Unidad 1

Introducción

La aleatoriedad es un concepto fundamental en la simulación de sistemas interactivos, ya que permite modelar comportamientos impredecibles y variabilidad en los sistemas. En esta unidad, explorarás cómo generar y utilizar números aleatorios en tus simulaciones, comprendiendo su importancia y aplicaciones. A través de ejemplos como los paseos aleatorios, aprenderás a implementar movimientos y comportamientos que emulan la aleatoriedad presente en la naturaleza. Este conocimiento te proporcionará las herramientas necesarias para desarrollar simulaciones más realistas y dinámicas.

¿Qué aprenderás en esta unidad?

Vas a explorar la aleatoriedad como una herramienta fundamental en la simulación de sistemas interactivos. Esta herramienta te permitirá producir comportamientos impredecibles y variabilidad.

Actividad 01

Arte generativo

Enunciado: vas a observar con detenimiento los siguientes videos y vas a reflexionar la relación que esto podría tener con tu perfil profesional:

Entrega: escribe un texto corto donde expliques qué potencial crees que pueda tener el arte generativo y algorítmico en tu perfil profesional.

🚀 Tu solución:

Mi perfil profesional y el arte generativo

Mi enfoque como Ingeniera en Diseño de Entretenimiento Digital está dirigido hacia el área estética y comunicativa de las experiencias interactivas. Soy fiel creyente de que una parte fundamental del proceso creativo detrás del desarrollo de un proyecto es permitirte experimentar con ideas divertidas que te permitan conectar con lo que haces. Por ello, el arte generativo y algorítmico me llama la atención.

Aunque la idea de comunicar mis ideas a través de código no es mi mayor fortaleza, las dinámicas detrás de la creación y cómo, a partir de parámetros, fórmulas matemáticas y curiosidad se pueden construir cosas tan locas y atrayentes me emociona.

Como diseñadora, contar con conocimientos en esta área es una gran ventaja, ya que me permite ser más versátil al plantear soluciones para las necesidades de los usuarios. Además, es una fuente de inspiración para desarrollar proyectos personales que me permitan explorar mis hobbies desde nuevas perspectivas.

Actividad 02

Diseño generativo

Enunciado: vas a observar con detenimiento el siguiente video que habla acerca del diseño generativo

GENERATIVE DESIGN, INTRO & Patrik Hübner

Recursos:

Entrega: escribe un texto corto donde reflexiones acerca de esta pregunta ¿Cómo se conecta lo anterior como mis intereses? O tal vez ¿Esto abre la puerta a la exploración de otras posibilidades?

🚀 Tu solución:

¿Cómo se conecta lo anterior con mis intereses? O tal vez ¿Esto abre la puerta a la exploración de otras posibilidades?

Bueno, mis intereses son muy variados, pero siento que, de alguna u otra manera, puedo conectarlos con proyectos creativos que involucren arte generativo. Me gusta mucho el arte abstracto y también quiero mejorar mis habilidades de ilustración. Sería increíble poder retratar animales o momentos específicos de mi vida a partir de código.

Además, me encanta la cocina, así que un recetario colaborativo no sería una mala idea. También he pensado en retomar el crochet, y sería genial recrear la textura de los tejidos de una manera divertida. Incluso podría volver a diseñar pósters, pero esta vez enfocándome en series y trabajando mejor la jerarquía del diseño.

Genuinamente veo muchas posibilidades. Aunque el código no sea mi especialidad, me encantaría experimentar con proyectos como estos, que están alineados con algunos de mis hobbies.

Investigación

Vas a indagar y a experimentar con los conceptos fundamentales de la unidad 0 del texto guía.

Actividad 03

🚀 Tu solución:

Caminatas aleatorias

Describe el experimento que vas a realizar.
- Qué pasaría si se crearan 2 walkers que inician en lados opuestos del lienzo de manera simultánea y son un poco más visibles que el original.
- Qué pasaría si estos dos walkers tienden a reunirse en el centro del canvas.
- Qué pasaría si después de reunirse en el centro emprenden de nuevo su camino aleatorio.
- Qué pasaría si todo lo anterioor ocurre con 8 walkers de diferentes colores.
¿Qué pregunta quieres responder con este experimento?
- ¿Cómo a partir de una base de código sencilla puedo crear un sistema de random walks?
¿Qué resultados esperas obtener?
- Espero que se forme una reunión divertida de random walks en torno al centro del canvas.
¿Qué resultados obtuviste?

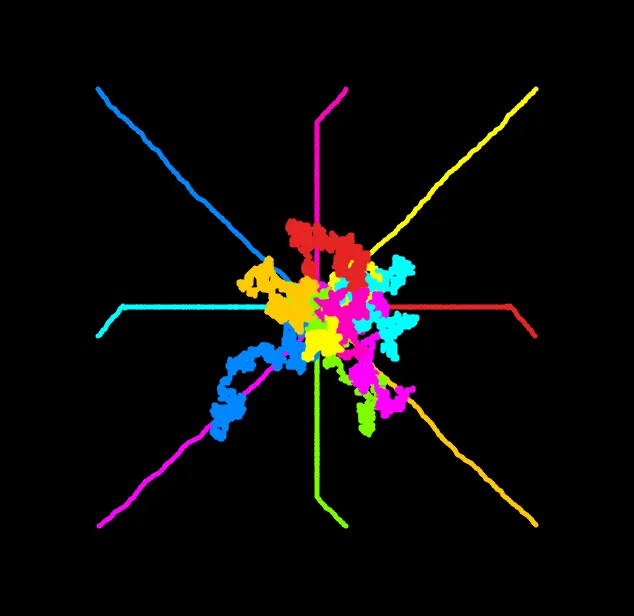
CodigoFinal

Código modificado

Enlace a la simulación aquí

let walker1, walker2, walker3, walker4, walker5, walker6, walker7, walker8;

let walker1Reversed = false;
let walker2Reversed = false;

function setup() {
  createCanvas(640, 640);
  walker1 = new Walker(100, 100, color(0, 134, 255));
  walker2 = new Walker(540, 540, color(255, 201,0));
  walker3 = new Walker(540, 100, color(255, 251, 0));
  walker4 = new Walker(100, 540, color(255, 0, 255));
  walker5 = new Walker(100, 350, color (0, 255, 572));
  walker6 = new Walker(540, 350, color (229,36,36));
  walker7 = new Walker(350, 100, color (255, 0, 193));
  walker8 = new Walker(350, 540, color (124,255,0));
  background(0);
}

function draw() {
  walker1.step();
  walker1.show();

  walker2.step();
  walker2.show();

  walker3.step();
  walker3.show();

  walker4.step();
  walker4.show();

  walker5.step();
  walker5.show();

  walker6.step();
  walker6.show();

  walker7.step();
  walker7.show();

  walker8.step();
  walker8.show();
}

class Walker {
  constructor(x, y, col) {
    this.x = x || width / 2;
    this.y = y || height / 2;
    this.color = col || color(0);
    this.reversed = false;
  }

  show() {
    stroke(this.color);
    strokeWeight(5);
    point(this.x, this.y);
  }

  step() {
    const centerX = width / 2;
    const centerY = height / 2;
    const threshold = 5; // Umbral de proximidad al centro

    // Detectar si el "walker" llega al centro
    if (!this.reversed && abs(this.x - centerX) <= threshold && abs(this.y - centerY) <= threshold) {
      this.reversed = true; // Cambiar a modo de movimiento opuesto
    }

    // Movimiento aleatorio opuesto después de llegar al centro
    if (this.reversed) {
      const choice = floor(random(4));
      if (choice === 0) {
        this.x += 2; // Movimiento más rápido
      } else if (choice === 1) {
        this.x -= 2;
      } else if (choice === 2) {
        this.y += 2;
      } else {
        this.y -= 2;
      }
    } else {
      // Movimiento hacia el centro con un pequeño desvío aleatorio
      if (this.x < centerX) this.x += floor(random(1, 3));
      else if (this.x > centerX) this.x -= floor(random(1, 3));

      if (this.y < centerY) this.y += floor(random(1, 3));
      else if (this.y > centerY) this.y -= floor(random(1, 3));
    }
  }
}

¿Qué aprendiste de este experimento?
- La construcción del resultado final fue progresiva, fui abordando una a una las curiosidades que se me presentaron y así pude entender cada una de las modificaciones que le realicé al código original. Como esta metodología me funcionó la seguiré implementando en las demás actividades

Actividad 04

Distribuciones de probabilidad

Enunciado: analiza detenidamente este ejemplo.

En tus palabras cuál es la diferencia entre una distribución uniforme y una no uniforme de números aleatorios. Modifica el código de la caminata aleatoria para que utilice una distribución no uniforme, favoreciendo el movimiento hacia la derecha.

Entrega:

Explicación de la diferencia entre distribuciones uniformes y no uniformes.
Código modificado y captura de pantalla de la caminata con distribución no uniforme.

🚀 Tu solución:

Diferencia entre distribuciones uniformes y no uniformes.
- Las distribuciones uniformes hacen que las probabilidades sean constantes, mientras que con las distribuciones no uniformes, las probabilidades son variables y tiendan hacia algunos valores más que hacia otros.

Distribuciones uniformes	Distribuciones no uniforme
Todos los valores dentro de un rango tienen la misma probabilidad de ser generados.	Los valores se generan con diferentes probabilidades, siguiendo una función de distribución específica.
Ejemplo: Usar random(0, 1) en p5.js genera valores donde cada número entre 0 y 1 tiene igual probabilidad.	Ejemplo: randomGaussian() en p5.js genera valores según una distribución normal (gaussiana), donde los números cercanos al promedio son más probables que los números extremos.

Código modificado

Enlace de la simulación aquí

Después de converger en el centro tienden hacia la derecha.

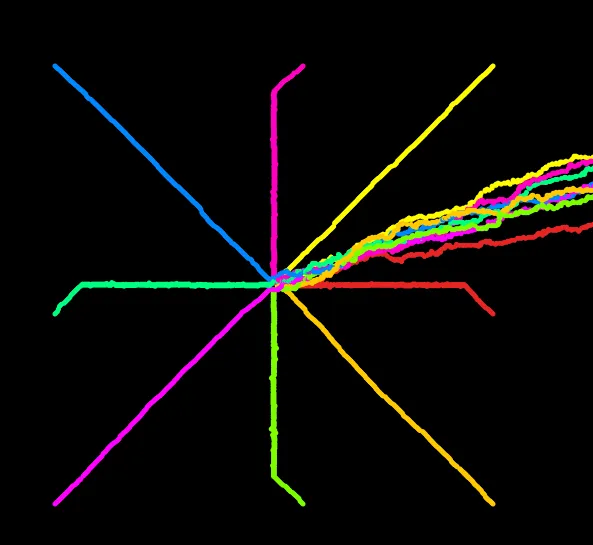
Actividad4

let walker1, walker2, walker3, walker4, walker5, walker6, walker7, walker8;

function setup() {
  createCanvas(640, 640);
  walker1 = new Walker(100, 100, color(0, 134, 255));
  walker2 = new Walker(540, 540, color(255, 201, 0));
  walker3 = new Walker(540, 100, color(255, 251, 0));
  walker4 = new Walker(100, 540, color(255, 0, 255));
  walker5 = new Walker(100, 350, color(0, 255, 127));
  walker6 = new Walker(540, 350, color(229, 36, 36));
  walker7 = new Walker(350, 100, color(255, 0, 193));
  walker8 = new Walker(350, 540, color(124, 255, 0));
  background(0);
}

function draw() {
  walker1.step();
  walker1.show();

  walker2.step();
  walker2.show();

  walker3.step();
  walker3.show();

  walker4.step();
  walker4.show();

  walker5.step();
  walker5.show();

  walker6.step();
  walker6.show();

  walker7.step();
  walker7.show();

  walker8.step();
  walker8.show();
}

class Walker {
  constructor(x, y, col) {
    this.x = x || width / 2;
    this.y = y || height / 2;
    this.color = col || color(0);
    this.reversed = false;
  }

  show() {
    stroke(this.color);
    strokeWeight(5);
    point(this.x, this.y);
  }

  step() {
    const centerX = width / 2;
    const centerY = height / 2;
    const threshold = 5; // Umbral de proximidad al centro

    // Detectar si el "walker" llega al centro
    if (!this.reversed && abs(this.x - centerX) <= threshold && abs(this.y - centerY) <= threshold) {
      this.reversed = true; // Cambiar a modo de movimiento opuesto
    }

    // Movimiento aleatorio no uniforme
    if (this.reversed) {
      // Favorecer el movimiento hacia la derecha usando randomGaussian()
      let dx = floor(randomGaussian(2, 1)); // Media de 2, desviación estándar de 1
      let dy = floor(randomGaussian(0, 1)); // Movimiento vertical más distribuido
      this.x += dx;
      this.y += dy;
    } else {
      // Movimiento hacia el centro con ajuste no uniforme
      let dx = randomGaussian(0, 1); // Distribución centrada en 0
      let dy = randomGaussian(0, 1);

      // Movimiento horizontal hacia el centro
      if (this.x < centerX) this.x += max(1, dx); // Asegurar un mínimo movimiento
      else if (this.x > centerX) this.x -= max(1, -dx);

      // Movimiento vertical hacia el centro
      if (this.y < centerY) this.y += max(1, dy);
      else if (this.y > centerY) this.y -= max(1, -dy);
    }
  }
}

Actividad 05

Distribución Normal

Enunciado: implementa un ejemplo que genere números aleatorios con una distribución normal (gaussiana). Visualiza la distribución utilizando figuras geométricas.

Entrega:

Código del ejemplo
Captura de pantalla
Una breve explicación de cómo se refleja la distribución normal en la visualización.

🚀 Tu solución:

Simulación aquí

actividad5

Código de ejemplo

let burbujas = [];
let ancho, alto;

function setup() {
  createCanvas(800, 400);
  ancho = width;
  alto = height;
  noStroke();
  background(255);
}

function draw() {
  background(240, 220); // Fondo con transparencia para efecto de desvanecimiento

  // Generar un número aleatorio con distribución normal
  let num = randomGaussian();
  let desviacion = 100;
  let media = width / 2;
  let x = num * desviacion + media;

  // Crear una nueva burbuja
  let nuevaBurbuja= {
    x: x,
    y: height,
    radio: random(6, 12),
    velocidad: random(1, 3),
    color: color(random(100, 255), random(10, 255), random(200, 255), 120)
  };
  burbujas.push(nuevaBurbuja);

  // Actualizar y dibujar burbujas
  for (let i = burbujas.length - 1; i >= 0; i--) {
    let b = burbujas[i];
    fill(b.color);
    ellipse(b.x, b.y, b.radio * 2);

    // Movimiento hacia arriba
    b.y -= b.velocidad;

    // Desaparecer si salen del lienzo
    if (b.y + b.radio < 0) {
      burbujas.splice(i, 1);
    }
  }
}

Reflejo de la distribución normal en la visualización

Las burbujas representan números aleatorios generados con una distribución normal (gaussiana). Su posición horizontal (x) refleja esta distribución: la mayoría de las burbujas se agrupan cerca del centro del lienzo, donde está la media, mientras que menos burbujas aparecen en los extremos, ya que los valores alejados de la media son menos frecuentes.

Actividad 06

Distribución personalizada: Lévy flight

Enunciado: realiza una simulación donde visualices un salta de Lévy.

Entrega:

En qué consiste el concepto de Lévy flight y en qué caso sería interesante usarlo.
Código de la simulación.
Captura de pantalla.

🚀 Tu solución:

Lévy flight

El concepto de Levy Flight es una forma de movimiento aleatorio que combina pasos cortos frecuentes con pasos largos ocasionales. Este comportamiento es muy diferente del movimiento aleatorio clásico (como un paseo aleatorio o random walk) porque incluye “saltos largos” que ocurren de forma menos frecuente pero tienen un impacto significativo en el desplazamiento total.

🫧 Casos interesantes para usarlo:

Arte generativo
- Patrones de Partículas Orgánicas: Crear simulaciones de enjambres o nubes de partículas con trayectorias impredecibles. Ejemplo: Representar un enjambre de luciérnagas donde algunas se alejan del grupo de manera ocasional.
- Diseño de Paisajes Naturales: Generar distribuciones de árboles, rocas o elementos naturales en un terreno. Ejemplo: En un bosque generado proceduralmente, los árboles podrían agruparse en ciertas áreas con dispersos puntos lejanos que simulan rarezas naturales.
- Pinturas Digitales Abstractas: Utilizalo para determinar la posición de trazos de pintura o gotas en un lienzo virtual. Ejemplo: Crear obras que imiten el comportamiento de tinta dispersa en papel húmedo, con salpicaduras ocasionales más grandes.
Sistemas Interactivos
- Comportamiento de Enemigos en Videojuegos: Usalo para que enemigos en un videojuego tengan patrones de movimiento impredecibles, dificultando al jugador anticipar su trayectoria. Ejemplo: Un jefe final que combina ataques cercanos frecuentes con movimientos rápidos y lejanos para sorprender al jugador.
- Sistemas de Dibujo Colaborativo: Implementar herramientas de dibujo digital donde las trayectorias de los pinceles tengan comportamientos orgánicos. Ejemplo: Una aplicación donde el usuario puede dibujar, pero las líneas ocasionalmente saltan a zonas inesperadas para fomentar la creatividad.

🌕 SIMULACIÓN

Enlace de la simulación aquí

Actividad6

Código

let fireflies = [];
let moon;
let attractToMoon = false; // Control booleano

function setup() {
  createCanvas(800, 800);
  moon = new Moon(width / 2, height / 2, 50);
  for (let i = 0; i < 20; i++) {
    fireflies.push(new Firefly(random(width), random(height)));
  }
}

function draw() {
  background(10, 10, 30);
  moon.display();

  for (let firefly of fireflies) {
    firefly.update();
    firefly.display();
  }
}

// Cambiar el estado del booleano cuando el cursor esté sobre el Sol
function mouseMoved() {
  let d = dist(mouseX, mouseY, moon.x, moon.y);
  attractToMoon = d < moon.r; // Se activa si el cursor está dentro del radio del Sol
}

class Moon {
  constructor(x, y, r) {
    this.x = x;
    this.y = y;
    this.r = r;
  }

  display() {
    noStroke();
    fill(255, 204, 0);
    ellipse(this.x, this.y, this.r * 2);
    // Simulated glow effect
    for (let i = 1; i < 10; i++) {
      fill(255, 255, 255, 100 / i);
      ellipse(this.x, this.y, this.r * 2 + i * 10);
    }
  }
}

class Firefly {
  constructor(x, y) {
    this.pos = createVector(x, y);
    this.vel = createVector(0, 0);
    this.acc = createVector(0, 0);
    this.radius = random(5, 8); // Tamaño de la luciérnaga
    this.maxSpeed = random(2, 4); // Velocidad máxima
    this.color = color(0, random(200, 255), random(10, 250), 200); // Amarillo verdoso
  }

  update() {
    // Aplicar Levy Flight
    let angle = random(TWO_PI);
    let step = this.levyFlight();
    this.acc = p5.Vector.fromAngle(angle).mult(step);

    // Aplicar fuerza central solo si attractToMoon es verdadero
    if (attractToMoon) {
      let moonForce = p5.Vector.sub(createVector(moon.x, moon.y), this.pos);
      moonForce.setMag(0.02); // Magnitud de la atracción al Sol
      this.acc.add(moonForce);
    }

    // Actualizar velocidad y posición
    this.vel.add(this.acc);
    this.vel.limit(this.maxSpeed);
    this.pos.add(this.vel);

    // Envolver bordes (toroidal)
    if (this.pos.x > width) this.pos.x = 0;
    if (this.pos.x < 0) this.pos.x = width;
    if (this.pos.y > height) this.pos.y = 0;
    if (this.pos.y < 0) this.pos.y = height;
  }

  levyFlight() {
    let r = random();
    if (r < 0.2) {
      // Pasos largos (ocasionales)
      return random(20, 50);
    } else {
      // Pasos cortos (frecuentes)
      return random(1, 5);
    }
  }

  display() {
    noStroke();
    fill(this.color);
    ellipse(this.pos.x, this.pos.y, this.radius);

    // Efecto de brillo
    fill(this.color, random(100, 150));
    ellipse(this.pos.x, this.pos.y, this.radius * 2);
  }
}

Las “luciérnagas” se se sienten atraídas hacia la luna, así que si el cursor se ubica sobre esta habrá una fuerza externa que las atraiga a ella.

Actividad 07

Ruido Perlin

Enunciado: utiliza el ruido Perlin para generar variaciones aleatorias pero suaves. Construye una aplicación que permita visualizar lo anterior.

Entrega:

Explica en tus propias palabras la figura 0.4: “A graph of Perlin noise values over time (left) and of random noise values over time (right)”
Explica cómo usaste el ruido Perlin para generar las variaciones.
El código.
Una captura de pantalla que muestre la visualización generada.

🚀 Tu solución:

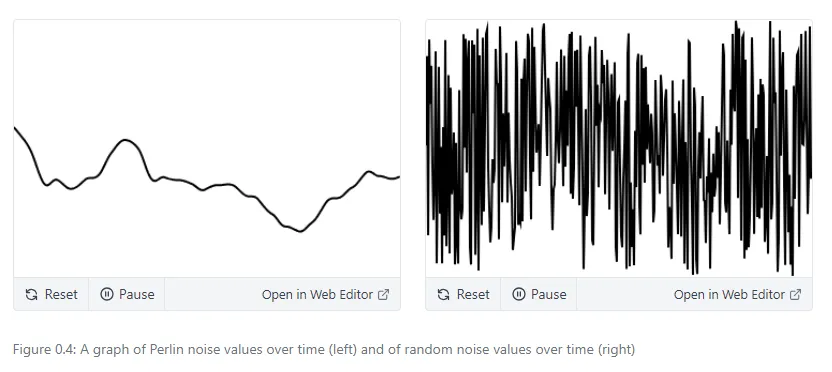
ruidoPerlin

La imagen de la izquierda, que representa el ruido de Perlín, muestra un gráfico más agradable a la vista, con variaciones ligeras entre sus trazos que generan una sensación de coherencia, fluidez y suavidad, por otro lado, la imagen de la derecha representa un gráfico generado con números aleatorios, que varían con mayor frecuencia creando esta sensación de acumulación de información en la que los datos varían drásticamente entre ellos.

🌻Jardín interactivo

Enlace a la simulación aquí

Empleé el ruido de Perlin para crear un jardín interactivo. Lo primero que se presenta es un canvas con algunos insectos revoloteando, la posición de cada insecto se calcula a partir de dos valores de ruido (uno para cada eje), noise(this.noiseX) y noise(this.noiseY) que generan valores entre 0 y 1 que son escalados al ancho y alto del lienzo, respectivamente. Esto produce un movimiento continuo y sin saltos, imitando el comportamiento errático pero fluido de un insecto real.

Al hacer click sobre el canvas se dibujan en él algunas flores, el ruido de Perlin ayuda en la generación de características visuales únicas para cada flor como el color de sus pétalos, el tamaño y hasta la cantidad de pétalos, características que no varían tanto debido a los pequeños saltos generados por el mismo ruido.

Flores: Cada flor tiene características únicas pero coherentes, simulando diversidad natural en colores y formas.

Insectos: Los insectos se mueven de manera fluida y aleatoria, replicando comportamientos biológicos observados en la naturaleza.

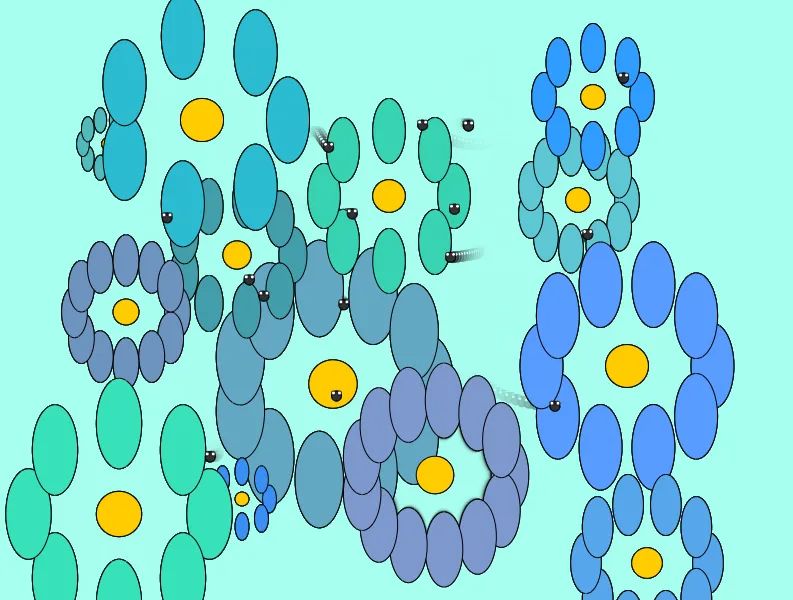
actividad

Código

let flowers = []; // Lista de flores
let insects = []; // Lista de insectos
let noiseOffset = 0; // Offset del ruido de Perlin para generar flores únicas

function setup() {
  createCanvas(800, 600);
  background(0, 255, 236); // Color de césped
  // Crear insectos iniciales
  for (let i = 0; i < 15; i++) {
    insects.push(new Insect(random(width), random(height), random(0.1, 1)));
  }
}

function draw() {
  background(166, 255, 242, 50); // Suavizado para simular un brillo tenue

  // Dibujar flores
  for (let flower of flowers) {
    flower.grow();
    flower.display();
  }

  // Dibujar insectos
  for (let insect of insects) {
    insect.move();
    insect.display();
  }
}

function mousePressed() {
  // Crear una nueva flor en la posición del mouse
  flowers.push(new Flower(mouseX, mouseY, noiseOffset));
  noiseOffset += 0.5; // Incrementar el ruido más significativamente
}

class Flower {
  constructor(x, y, noiseOffset) {
    this.x = x;
    this.y = y;
    this.noiseOffset = noiseOffset;
    this.size = 0; // Tamaño inicial de la flor
    this.maxSize = random(20, 100); // Tamaño máximo basado en un rango aleatorio

    // Ajuste para variar la cantidad de pétalos de forma más visible
    this.petalCount = floor(map(noise(noiseOffset), 0, 1, 5, 15));

    this.petalColor = color(
      noise(noiseOffset) * 155,
      100 + noise(noiseOffset + 1) * 155,
      100 + noise(noiseOffset + 2) * 255
    ); // Color basado en el ruido
    this.centerColor = color(255, 204, 0); // Centro amarillo cálido
  }

  grow() {
    if (this.size < this.maxSize) {
      this.size += 0.5; // Crecimiento gradual
    }
  }

  display() {
    push();
    translate(this.x, this.y);
    for (let i = 0; i < this.petalCount; i++) {
      let angle = TWO_PI / this.petalCount * i;
      let petalX = cos(angle) * this.size;
      let petalY = sin(angle) * this.size;
      fill(this.petalColor);
      ellipse(petalX, petalY, this.size / 2, this.size); // Pétalos alargados
    }
    fill(this.centerColor);
    ellipse(0, 0, this.size / 2); // Centro de la flor
    pop();
  }
}

class Insect {
  constructor(x, y, speed) {
    this.x = x;
    this.y = y;
    this.speed = speed; // Velocidad de movimiento del insecto
    this.noiseX = random(1000); // Offset único para el movimiento en X
    this.noiseY = random(1000); // Offset único para el movimiento en Y
  }

  move() {
    this.x = noise(this.noiseX) * width; // Movimiento horizontal suave
    this.y = noise(this.noiseY) * height; // Movimiento vertical suave
    this.noiseX += 0.01 * this.speed; // Incrementar el ruido para simular movimiento
    this.noiseY += 0.01 * this.speed;
  }

  display() {
    fill(50, 50, 50); // Color del insecto
    ellipse(this.x, this.y, 10, 10); // Cuerpo del insecto
    fill(255);
    ellipse(this.x - 3, this.y - 3, 4, 4); // Ala izquierda
    ellipse(this.x + 3, this.y - 3, 4, 4); // Ala derecha
  }
}

Aplicación

Vas a aplicar los conceptos con los que experimentaste en la fase de investigación para diseñar y desarrollar una aplicación interactiva en tiempo real.

Actividad 08

Diseño: exploración de la idea

Enunciado: diseña una aplicación interactiva en tiempo que utilice los conceptos que investigaste. La aplicación debe:

Generar una pieza de arte generativo algorítmico.
Debes usar al menos TRES conceptos.
El contenido generado debe ser interactivo. Puedes utilizar mouse, teclado, cámara, micrófono, etc, para variar los parámetros del algoritmo en tiempo real.

Entrega:

Un texto donde expliques tu intención de diseño.
¿Cómo piensas usar los tres conceptos y por qué estos?
Reporta los referentes que usaste para inspirarte.

🚀 Tu solución:

Fiesta de partículas

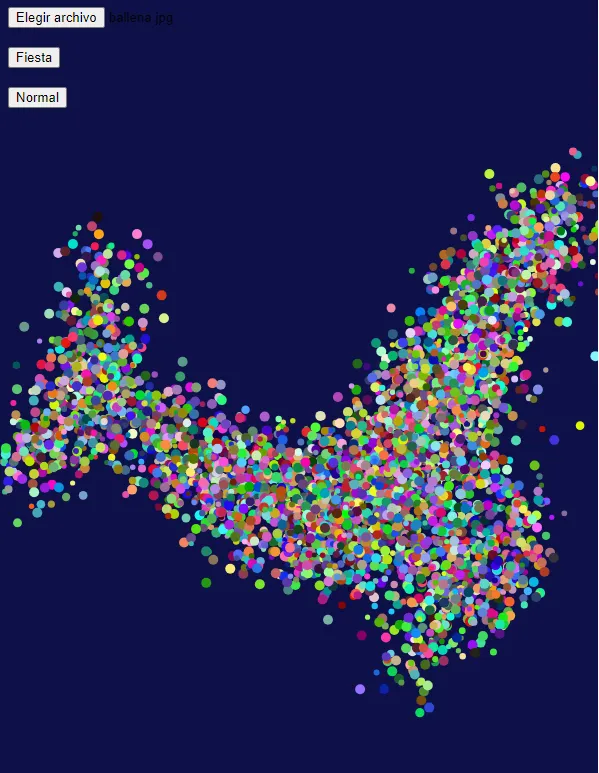
El proyecto será de exploración de partículas y cómo podemos crear formas divertidas con ellas. El usuario seleccionará desde su dispositivo algunas siluetas (preferiblemente de animales marinos) y las partículas rastrearán esta imagen y tratarán de imitarla por medio de su distribución en el canvas. Además, habrá un botón llamado “Fiesta🥳” que podrá crear un efecto divertido sobre el tamñano, colores y la distribución de las partículas; y un botón “Normal” para volver a la simulación.

¿Cómo piensas usar los tres conceptos y por qué estos?

Random Gaussean (distribución normal) —> Colores de las partículas para que se mantengan dentro de una misma gama de color.
Random walk—> Color del fondo para generar un efecto de viveza al canvas, lo pensé como un acuario que dependiendo de la luz que reciba del sol va a tener un azul más o menos profundo y el random walk hace que el cambio de color no sea abrupto.
Levy fligth---> Activado mediante el botón fiesta, podría crear un ambiente divertido al cambiar los colores, el tamaño y el comportamiento de las partículas con los saltos cortos frecuentes y los largos ocasionales.

Reporta los referentes que usaste para inspirarte.

Referencia unidad 1

Patch de partículas en cables link aquí

Cambio a modo “fiesta” inspirado en el trabajo de Emanuel :)

Actividad 09

Materialización

Enunciado: vas a implementar tu aplicación diseñada.

Entrega:

Código de la aplicación.
Captura del contenido generado.
En caso de realizar alguna variación al concepto original, escribe un texto donde expliques la razón del cambio.

🚀 Tu solución:

Fiesta de partículas

Enlace del proyecto aquí

Imagen original

ballena original

Imagen Modo Normal

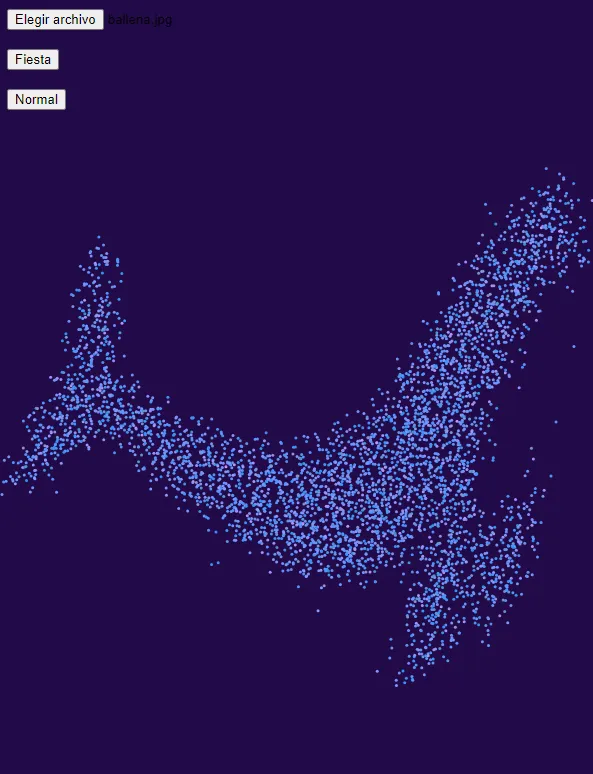
ballena normal

Imagen Modo Fiesta

ballena fiesta

Código

let img;
let particles = [];
let imgData = [];
let input;
let bgColor; // Color de fondo dinámico
let fiesta = false;
let buttonFiesta, buttonNormal;

function setup() {
  createCanvas(600, 800);
  background(0);
  input = createFileInput(handleFile);
  input.position(10, 10);

  buttonFiesta = createButton('Fiesta');
  buttonFiesta.position(10, 50);
  buttonFiesta.mousePressed(() => toggleFiesta(true));

  buttonNormal = createButton('Normal');
  buttonNormal.position(10, 90);
  buttonNormal.mousePressed(() => toggleFiesta(false));

  // Inicializamos el color de fondo en un azul oscuro
  bgColor = createVector(10, 20, 80);
}

function handleFile(file) {
  if (file.type === 'image') {
    img = loadImage(file.data, () => {
      processImage();
    });
  }
}

function processImage() {
  image(img, 0, 0, width, height);
  loadPixels();

  imgData = [];
  for (let x = 0; x < width; x += 4) {  // Mayor precisión reduciendo el paso
    for (let y = 0; y < height; y += 4) {
      let index = (x + y * width) * 4;
      let brightness = pixels[index] + pixels[index + 1] + pixels[index + 2];
      if (brightness < 400) {  // Filtrar puntos oscuros de la imagen
        imgData.push(createVector(x, y));
      }
    }
  }

  particles = [];
  for (let i = 0; i < imgData.length; i++) {
    particles.push(new Particle(random(width), random(height), imgData[i]));
  }
}

function draw() {
  updateBackground(); // Actualizar el color de fondo con random walk
  background(bgColor.x, bgColor.y, bgColor.z);

  for (let p of particles) {
    p.update();
    p.show();
  }
}

function updateBackground() {
  // Random walk en la gama de azules oscuros
  bgColor.x = constrain(bgColor.x + random(-5, 5), 0, 50);   // Mantener tonos oscuros en R
  bgColor.y = constrain(bgColor.y + random(-5, 5), 0, 50);   // Mantener tonos oscuros en G
  bgColor.z = constrain(bgColor.z + random(-10, 10), 50, 150); // Azul oscuro variable
}

function toggleFiesta(state) {
  fiesta = state;
  if (fiesta) {
    // Cambiar colores a modo fiesta
    for (let p of particles) {
      p.r = random(255);
      p.g = random(255);
      p.b = random(255);
    }
  } else {
    // Restaurar colores y tamaños originales
    for (let p of particles) {
      p.r = constrain(randomGaussian(100, 30), 50, 200);
      p.g = 150;
      p.b = constrain(randomGaussian(255, 20), 200, 255);
      p.size = 3;
    }
  }
}

class Particle {
  constructor(x, y, target) {
    this.pos = createVector(x, y);
    this.target = target;
    this.vel = p5.Vector.random2D();
    this.acc = createVector();
    this.maxSpeed = 2;
    this.size = 3;

    // Distribución normal para el color de las partículas
    this.r = constrain(randomGaussian(100, 30), 50, 200);
    this.g = 150;
    this.b = constrain(randomGaussian(255, 20), 200, 255);
  }

  update() {
    if (fiesta) {
      // Movimiento caótico con vuelo de Lévy
      let step = pow(random(1), -1.5);
      let angle = random(TWO_PI);
      this.vel.x = cos(angle) * step;
      this.vel.y = sin(angle) * step;
      this.size = constrain(2 + step * 3, 2, 10); // Variar tamaño con Lévy Flight
    } else {
      let force = p5.Vector.sub(this.target, this.pos);
      force.setMag(0.1);
      this.acc.add(force);

      // Reducir gradualmente el tamaño si está en modo normal
      this.size = lerp(this.size, 3, 0.1);
    }

    this.vel.add(this.acc);
    this.vel.limit(this.maxSpeed);
    this.pos.add(this.vel);
    this.acc.mult(0);
  }

  show() {
    fill(this.r, this.g, this.b);
    noStroke();
    ellipse(this.pos.x, this.pos.y, this.size, this.size);
  }
}

Consolidación y matacognión

Ahora que has experimentado con la aleatoriedad y has aplicado estos conceptos en una pieza de arte generativo, es momento de reflexionar sobre el proceso y los resultados obtenidos.

Actividad 10

Análisis de resultados

Enunciado: revisa los resultados de las actividades de la fase APPLY. ¿Qué desafíos encontraste al aplicar los conceptos aprendidos? ¿Qué aprendiste de estos desafíos?

Entrega: descripción de los desafíos encontrados y las lecciones aprendidas durante la fase APPLY.

🚀 Tu solución:

Desafíos a los que me enfrente en la fase APPLY

Cuando debía aplicar los concepto aprendidos en la fase SEEK, me enfrenté a un bloqueo creativo. No sabía de qué manera divertida abordar estos temas, busqué algunas referencias pero nada me convencía del todo. La primera idea fue la de hacer un acuario con peces y burbujas que interactuaran entre sí pero no terminaba de convencerme la interacción del usuario. Finalmente, recurrí a inspirarme de proyectos hecho en Cables.gl, una página web con la que pude experimentar el semestre pasado y fue así como encontré un proyecto que me iluminó el camino.
Después de inspirarame, inicié a experimentar para ver si podía replicar de cierta manera la interacción de las partículas de Cables en P5.js, sin embargo, el proyecto que me inspiró contenía a las partículas en un espacio tridimensional así que tuve que modificar algunos factores para el funcionamiento de mi proyecto.

Lecciones aprendidas de la fase APPLY

Para mí, crear diferentes versiones de una misma idea o concepto me ayuda a crear un producto final más completo y divertido.
Aunque Cables.gl sea una plataforma diferente es una gran fuente de inspiración para explorar con el arte generativo.

Actividad 11

Conexión con Diseño de Entretenimiento Digital

Enunciado: describe cómo los conceptos de aleatoriedad, distribuciones y ruido Perlin pueden ser utilizados en el diseño de videojuegos, experiencias interactivas o animaciones. Da ejemplos concretos.

Entrega: descripción de al menos tres aplicaciones de los conceptos aprendidos en el diseño de entretenimiento digital, con ejemplos concretos.

🚀 Tu solución:

Aplicaciones de los conceptos aprendidos en experiencias interactivas

1. Ruido de Perlin: Sirve para generar texturas procedurales y elementos dinámicos que pueden emplearse en escenarios y montajes de experiencias. Los videojuegos y experiencias interactivas a menudo necesitan generar mundos dinámicos sin depender completamente de diseños predefinidos. El ruido Perlin se usa para crear terrenos, texturas y patrones naturales de manera fluida y coherente.

Ejemplo: En una instalación interactiva con proyección en un domo, el paisaje generado responde al movimiento de los usuarios. Usando ruido Perlin, se puede modificar la topografía de montañas o la disposición de vegetación de forma suave y realista, evitando la artificialidad del ruido aleatorio puro.

2. Vuelos de Lévy

El movimiento de personajes o elementos en entornos interactivos puede beneficiarse de modelos estadísticos más complejos que la simple aleatoriedad uniforme. Un enfoque es el uso de distribuciones normales para animaciones suaves o vuelos de Lévy para movimientos caóticos e impredecibles.

Ejemplo: En una instalación donde partículas de luz siguen a los usuarios en una pantalla interactiva, en vez de moverse de forma lineal, pueden tener variaciones usando una el vuelo de Levy, haciendo que su seguimiento parezca más divertido y dinámico.

3. Distribuciones de probabilidad

Las distribuciones de probabilidad pueden ser utilizadas para modelar el comportamiento de personajes no jugadores (NPCs), enemigos o entidades en un juego. En lugar de moverse de forma completamente aleatoria, se pueden emplear distribuciones normales o personalizadas para definir patrones de movimiento más realistas.

Ejemplo: En juegos de sigilo como The Last of Us, las patrullas enemigas no siguen un patrón fijo, sino que su comportamiento es influenciado por distribuciones de probabilidad que definen con qué frecuencia revisan ciertas áreas o cómo reaccionan ante estímulos del entorno.

Actividad 12

Reflexión sobre el proceso de aprendizaje

Enunciado: reflexiona sobre tu propio proceso de aprendizaje durante esta unidad. ¿Qué estrategias te resultaron más efectivas para comprender los conceptos? ¿Qué podrías mejorar en futuras unidades?

Entrega:

Descripción de las estrategias de aprendizaje utilizadas y su efectividad.
Planteamiento de mejoras para futuras unidades.

🚀 Tu solución:

Estrategias de aprendizaje utilizadas

Crear analogías entre los conceptos y actividades cotidianas para comprenderlos de manera más sencilla.
Practicar los conceptos con temas que me interesen, por ejemplo: quisiera comenzar a dibujar animales marinos, ¿cómo podría hacerlo con los conceptos que estoy aprendiendo?
Pensar en buscar referencias divertidas que al verlas me haga querer intervenirlas a mi manera.

Planteamiento de mejoras para futuras unidades.

Para futuras unidades quisiera seguir haciendo proyectos divertidos relacionados con mis hobbies, así que un consejo para mi yo del futuro es buscar referencias visuales que se salgan de mi zona de confort o sitios recurrentes para así poder experimenta y arriesgarme más.

Actividad 13

Autoevaluación

Enunciado: evalúa tu nivel de comprensión de los conceptos de la unidad en una escala del 1 al 5 (1: Nada de comprensión, 5: Dominio completo). Justifica tu autoevaluación con ejemplos concretos de tu trabajo en la unidad. Identifica áreas donde necesitas reforzar tu aprendizaje.

Entrega:

Autoevaluación con justificación y ejemplos concretos.
Identificación de áreas de mejora.

🚀 Tu solución:

Escala de comprensión

Me asigno un nivel de 4, comprendo los conceptos y puedo aplicarlos a proyectos de manera dinámica aprovechando los beneficios de cada uno pero personalemnte considero que debo practicar un poco más en otros proyectos similares al planteado en la actividad 8 para así sentirme más confiada a la hora de aplicarlos en mis proyecto. El concepto que tal vez me causa más curiosidad sobre cómo implementarlo es el Lévy flight pues en mi proyecto lo empleé en el modo fiesta, quisiera usarlo de varias maneras para sacarle más provecho sin que sea solo un modo a parte de aleatoriedad.