Unidad 2

Introducción

En esta unidad, te sumergirás en el fascinante mundo de los vectores, las fuerzas invisibles que dan vida a tus creaciones digitales. Experimentarás con conceptos matemáticos y físicos, como velocidad y aceleración, para controlar el movimiento en tus proyectos interactivos. Aprenderás a manipular vectores en p5.js, pero recuerda que este conocimiento es aplicable a cualquier lenguaje de programación.

¿Qué aprenderás en esta unidad?

En esta fase, vas a revisar algunos conceptos básicos de vectores que ya conoces tu paso por ciencia básica.

Actividad 01

Analiza una aplicación interactiva

Enunciado: analiza el ejemple: Example 1.2: Bouncing Ball with Vectors!

• ¿Cómo funciona la suma dos vectores?
• ¿Por qué esta línea position = position + velocity; no funciona?

Entrega: escribe en tu bitácora la solución a las preguntas anteriores.

🚀 Tu solución:

Estudiante

Suma de vectores

La suma de dos vectores se puede hacer de manera muy sencilla utilizando el objeto createVector(), que permite trabajar con vectores. Para sumar dos vectores, solo debes sumar sus componentes correspondientes (es decir, la componente X con la componente X y la componente Y con la componente Y).

¿La línea position = position + velocity;?

La línea position = position + velocity; no funciona porque los vectores no se pueden sumar de esa manera directamente. Las variable position y velocity son vectores, y no puedes simplemente sumarlos con el operador + como lo harías con números simples.

Para sumar vectores, debes usar el método .add() que está disponible en los objetos ”.Vector”. Este método se asegura de que cada componente (X, Y, Z si fuera el caso) se sume correctamente.

position = position + velocity; // Incorrecto

position.add(velocity); // Correcto

Solución

Retroalimentación

Actividad 02

Repasa

Enunciado: realiza este ejercicio del libro Exercise 1.1

• ¿Que tuviste que hacer para hacer la conversión propuesta?

Entrega: el código del ejercicio.

🚀 Tu solución:

Estudiante

let walker;

function setup() {
  createCanvas(640, 240);
  walker = new Walker();
  background(255);
}

function draw() {
  walker.step();
  walker.show();
}

class Walker {
  constructor() {
    // Inicializa la posición con un vector
    this.position = createVector(width / 2, height / 2);
  }

  show() {
    stroke(0);
    point(this.position.x, this.position.y); // Usamos los componentes del vector
  }

  // El walker se mueve usando un vector aleatorio
  step() {
    // Crea un vector aleatorio para el paso
    let step = createVector(random(-2.75, 3), random(-2.75, 3));

    // Suma el paso al vector de la posición
    this.position.add(step);
  }
}

Solución

Retroalimentación

Investigación

¡Es hora de explorar! En esta fase, profundizarás en la teoría y práctica de los vectores a través de la lectura del capítulo 1 del libro “The Nature of Code”. Realizarás experimentos, analizarás ejemplos y te familiarizarás con las diferentes funciones de p5.js para manipular vectores.

Actividad 03

Experimenta

Enunciado: dale una mirada a este código

let position;

function setup() {
    createCanvas(400, 400);
    posicion = createVector(6,9);
    playingVector(posicion);
    noLoop();
}

function playingVector(v){
    v.x = 20;
    v.y = 30;
}

function draw() {
    background(220);
    console.log("Only once");
}

Para este experimento puedes usar las funciones console.log() y print() para imprimir mensajes en la consola del navegador. También puedes usar el método toString() de la clase p5.Vector para imprimir el vector en la consola.

• ¿Qué resultado esperas obtener?
• ¿Qué resultado obtuviste?
• Recuerda los conceptos de paso por valor y paso por referencia en programación. Muestra ejemplos de este concepto en javascript.
• ¿Qué tipo de paso se está realizando en el código?
• ¿Qué aprendiste?

Entrega: la solución a las preguntas.

🚀 Tu solución:

Estudiante

¿Qué resultado esperas obtener?

Que aparezca en consola “Only once”

¿Qué resultado obtuviste?

Pinto de gris y salio en texto en consola

1. Paso por Valor:

Definición: Cuando un valor es pasado por valor a una función, se pasa una copia del valor. Es decir, cualquier cambio hecho en la variable dentro de la función no afecta la variable original fuera de la función. Aplicación: Este comportamiento se aplica a los tipos primitivos en JavaScript, como números, cadenas de texto, booleanos, undefined, null, etc.

Ejemplo:

function cambiarValor(x) {
    x = 10;
    console.log("Dentro de la función:", x); // Imprime 10
}

let a = 5;
cambiarValor(a);
console.log("Fuera de la función:", a); // Imprime 5

2. Paso por Referencia:

Definición: Cuando un valor es pasado por referencia a una función, se pasa una referencia al objeto en memoria. Esto significa que cualquier cambio realizado en el objeto dentro de la función sí afectará al objeto original. Aplicación: Este comportamiento se aplica a los tipos de objetos en JavaScript, como objetos literales, arrays, funciones, y también instancias de clases.

Ejemplo:

function cambiarPropiedad(obj) {
    obj.nombre = "Juan";
    console.log("Dentro de la función:", obj.nombre); // Imprime 'Juan'
}

let persona = { nombre: "Carlos" };
cambiarPropiedad(persona);
console.log("Fuera de la función:", persona.nombre); // Imprime 'Juan'

¿Qué tipo de paso se está realizando en el código?

Paso por referencia, porque el vector posicion (un objeto) se pasa a la función y cualquier modificación que se haga dentro de la función afecta directamente al objeto original fuera de ella.

¿Qué aprendiste?

Como funcionan los conceptos de pasos por valor y refencia a la hora de programar y como aplicarlos.

Solución

Retroalimentación

Actividad 04

Explora posibilidades

Enunciado: dale una mirada a la clase p5.Vector aquí.

• ¿Para qué sirve el método mag()? Nota que hay otro método llamado magSq(). ¿Cuál es la diferencia entre ambos? ¿Cuál es más eficiente?
• ¿Para qué sirve el método normalize()?
• Te encuentras con un periodista en la calle y te pregunta ¿Para qué sirve el método dot()? ¿Qué le responderías en un frase?
• El método dot() tiene una versión estática y una de instancia. ¿Cuál es la diferencia entre ambas?
• Ahora el mismo periodista curioso de antes te pregunta si le puedes dar una intuición geométrica acerca del producto cruz. Entonces te pregunta ¿Cuál es la interpretación geométrica del producto cruz de dos vectores? Tu respuesta debe incluir qué pasa con la orientación y la magnitud del vector resultante.
• ¿Para que te puede servir el método dist()?
• ¿Para qué sirven los métodos normalize() y limit()?

Entrega: la solución a las preguntas

🚀 Tu solución:

Estudiante

¿Para qué sirve el método mag()?

El método mag() devuelve la magnitud (o longitud) de un vector, es decir, su distancia desde el origen (0, 0) hasta el punto que representa. Es equivalente a calcular la raíz cuadrada de la suma de los cuadrados de sus componentes (como el teorema de Pitágoras).

¿Cuál es la diferencia entre mag() y magSq()?

mag(): Devuelve la magnitud del vector (raíz cuadrada de la suma de los cuadrados de sus componentes). magSq(): Devuelve el cuadrado de la magnitud, lo que evita calcular la raíz cuadrada, lo cual puede ser más eficiente en términos de rendimiento.

¿Cuál es más eficiente?

magSq() es más eficiente porque no tiene que calcular la raíz cuadrada.

¿Para qué sirve el método normalize()?

normalize() ajusta un vector para que tenga una magnitud de 1, es decir, lo convierte en un vector unitario. No cambia la dirección del vector, solo su tamaño.

El método dot(), ¿qué le responderías a un periodista?

El método dot() calcula el producto punto entre dos vectores, lo que nos da una medida de cuán alineados están esos vectores. Si el producto punto es 0, los vectores son perpendiculares.

¿Cuál es la diferencia entre la versión estática y la de instancia de dot()?

Estática (p5.Vector.dot(v1, v2)): Se llama sin necesidad de un objeto, pasando los dos vectores como parámetros.

De instancia (v1.dot(v2)): Se llama sobre un vector específico, con el otro vector como argumento.

##¿Cuál es la interpretación geométrica del producto cruz? El producto cruz de dos vectores en 3D genera un vector perpendicular a los dos vectores originales. La magnitud de este vector es igual al área del paralelogramo formado por los dos vectores, y su orientación sigue la regla de la mano derecha. Si los vectores están alineados, el producto cruz es el vector nulo (0,0,0).

¿Para qué te puede servir el método dist()?

dist() calcula la distancia euclidiana entre dos puntos en el espacio. Es útil cuando necesitas saber qué tan lejos están dos puntos en un plano o en el espacio.

¿Para qué sirven los métodos normalize() y limit()?

normalize(): Como mencionamos antes, convierte un vector en un vector unitario, es decir, lo reduce a una magnitud de 1 sin cambiar su dirección. limit(): Restringe la magnitud de un vector a un valor máximo dado. Si la magnitud del vector es mayor que el límite, se reduce al valor especificado. Es útil cuando quieres evitar que un vector sea demasiado grande.

Solución

Retroalimentación

Actividad 05

Interpolamos?

Enunciado: vas a tomar como inspiración este ejemplo de la referencia de p5.js:

function setup() {
    createCanvas(100, 100);
}

function draw() {
    background(200);

    let v0 = createVector(50, 50);
    let v1 = createVector(30, 0);
    let v2 = createVector(0, 30);
    let v3 = p5.Vector.lerp(v1, v2, 0.5);
    drawArrow(v0, v1, 'red');
    drawArrow(v0, v2, 'blue');
    drawArrow(v0, v3, 'purple');
}

function drawArrow(base, vec, myColor) {
    push();
    stroke(myColor);
    strokeWeight(3);
    fill(myColor);
    translate(base.x, base.y);
    line(0, 0, vec.x, vec.y);
    rotate(vec.heading());
    let arrowSize = 7;
    translate(vec.mag() - arrowSize, 0);
    triangle(0, arrowSize / 2, 0, -arrowSize / 2, arrowSize, 0);
    pop();
}

Vas a modificarlo para generar este resultado:

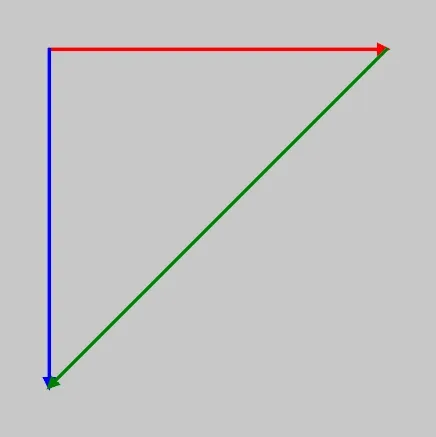
• Analiza cómo funciona el método lerp().
• Nota que además de la interpolación lineal de vectores, también puedes hacer interpolación lineal de colores con el método lerpColor().

Dedica un tiempo a estudiar cómo se dibuja una flecha en el método drawArrow().

Entrega:

• El código que genera el resultado propuesto.
• ¿Cómo funciona lerp() y lerpColor().
• ¿Cómo se dibuja una flecha usando drawArrow()?

🚀 Tu solución:

Estudiante

let v3;
let t = 0;

function setup() {
    createCanvas(400, 400);
}

function draw() {
    background(200);

    let v0 = createVector(50, 50); // Origen
    let v1 = createVector(200, 0); // Vector 1
    let v2 = createVector(0, 200); // Vector 2

    let v1_end = v0.copy().add(v1);
    let v2_end = v0.copy().add(v2);
    let v4 = v2_end.copy().sub(v1_end); // Vector 4

    v3 = p5.Vector.lerp(v1, v2, t); // Vector 3 en relación a v1, v2 y el tiempo

    t += 0.01;
    if (t > 1) t = 0;

    drawArrow(v0, v1, 'red');
    drawArrow(v0, v2, 'blue');
    drawArrow(v0, v3, 'purple');
    drawArrow(v1_end, v4, 'green');

}

function drawArrow(base, vec, myColor) {
    push();
    stroke(myColor);
    strokeWeight(3);
    fill(myColor);
    translate(base.x, base.y);
    line(0, 0, vec.x, vec.y);
    rotate(vec.heading());
    let arrowSize = 7;
    translate(vec.mag() - arrowSize, 0);
    triangle(0, arrowSize / 2, 0, -arrowSize / 2, arrowSize, 0);
    pop();
}

Solución

Retroalimentación

Actividad 06

Hagamos que todo se mueva

Enunciado: modifica de nuevo el programa de la actividad anterior, pero esta vez cambia la base de las flechas y la escala de los vectores usando el mouse.

Entrega:

• Código con la modificación.
• Explica cómo solucionaste el problema.

🚀 Tu solución:

Estudiante

let v3;
let t = 0;

function setup() {
    createCanvas(300, 300);
}

function draw() {
    background(200);

    let v0 = createVector(mouseX, mouseY);
    let scaleFactor = calculateScaleFactor(mouseX, mouseY);

    let v1 = createVector(120 * scaleFactor, 0);
    let v2 = createVector(0, 120 * scaleFactor);

    let v1_end = v0.copy().add(v1);
    let v2_end = v0.copy().add(v2);
    let v4 = v2_end.copy().sub(v1_end);

    v3 = p5.Vector.lerp(v1, v2, t);

    t += 0.01;
    if (t > 1) t = 0;

    drawArrow(v0, v1, 'red');
    drawArrow(v0, v2, 'blue');
    drawArrow(v0, v3, 'purple');
    drawArrow(v1_end, v4, 'green');
}

function calculateScaleFactor(x, y) {
    return dist(x, y, width / 2, height / 2) / 100;
}

function drawArrow(base, vec, myColor) {
    push();
    stroke(myColor);
    strokeWeight(3);
    fill(myColor);
    translate(base.x, base.y);
    line(0, 0, vec.x, vec.y);
    rotate(vec.heading());
    let arrowSize = 7;
    translate(vec.mag() - arrowSize, 0);
    triangle(0, arrowSize / 2, 0, -arrowSize / 2, arrowSize, 0);
    pop();
}

Solución

Retroalimentación

Actividad 07

Motion 101

Entrega: ahora vas a leer y analizar con mucho detenimiento la sección Motion with vectors. El autor propone un marco de movimiento llamado motion 101.

¿En qué consiste motion 101?

Entrega: la respuesta a la pregunta e ilustra con un ejemplo.

🚀 Tu solución:

Estudiante

El algoritmo Motion 101 primero, tiene un objeto Mover tiene dos datos, posición y velocidad, ambos objetos p5.Vector. Estos se inicializan en el constructor del objeto. En este caso, decidiré arbitrariamente inicializar el objeto Mover dándole una posición y velocidad aleatorias. Tenga en cuenta el uso de esto con todas las variables que forman parte del objeto Mover. El objeto Mover necesita moverse (aplicando su velocidad a su posición) y debe ser visible. Implementaré estas necesidades como funciones denominadas update() y show(). Pondré todo el código de lógica de movimiento en update() y dibujaré el objeto en show()

Ejemplo:

let mover;

function setup() {
  createCanvas(400, 400);
  mover = new Mover();
}

function draw() {
  background(220);
  mover.update();
  mover.checkEdges();
  mover.show();
}

class Mover {
  constructor() {
    this.position = createVector(random(width), random(height));
    this.velocity = createVector(random(-2, 2), random(-2, 2));
  }

  update() {
    this.position.add(this.velocity);
  }

  show() {
    stroke(0);
    fill(175);
    circle(this.position.x, this.position.y, 48);
  }

  checkEdges() {

    if (this.position.x > width) {
      this.position.x = 0;
    } else if (this.position.x < 0) {
      this.position.x = width;
    }

    if (this.position.y > height) {
      this.position.y = 0;
    } else if (this.position.y < 0) {
      this.position.y = height;
    }
  }
}

Solución

Retroalimentación

Actividad 08

Experimenta

Enunciado: realiza un experimento para basado en el ejemplo 1.7.

• Entiende el ejemplo.
• Vas a proponer una modificación mediante esta pregunta que te harás: ¿Qué pasa si…?
• ¿Qué te imaginas que pasará?
• ¿Qué pasó?
• ¿Por qué?
• Concluye

Entrega: la respuesta a las cuestiones anteriores.

🚀 Tu solución:

Estudiante

Cambios realizados:

Cambio en la velocidad al tocar los bordes: Ahora, cuando el objeto toca cualquiera de los bordes (izquierda, derecha, arriba o abajo), la velocidad del objeto se ajusta de manera aleatoria. Esto significa que la dirección y la rapidez del objeto pueden cambiar cada vez que rebote en el borde del canvas.

Resultado esperado:

Movimiento más impredecible: Con este cambio, el objeto mover ya no se moverá de manera continua y predecible a través del canvas. Cada vez que toque un borde, su velocidad cambiará de manera aleatoria, lo que provocará que el objeto se mueva de manera más errática.

Efecto visual: El movimiento será menos suave y más impredecible, ya que cada vez que el objeto toque un borde, podría empezar a moverse más rápido o más lento, o incluso cambiar de dirección de manera completamente aleatoria. Esto puede crear un patrón de movimiento más “caótico” en el lienzo.

// Declare the Mover object.
let mover;

function setup() {
  createCanvas(640, 240); // Creamos un lienzo de 640x240 píxeles
  // Create the Mover object.
  mover = new Mover(); // Inicializamos el objeto mover
}

function draw() {
  background(255); // Limpiamos el lienzo con un color blanco en cada frame

  // Llamamos a los métodos del objeto mover
  mover.update();      // Actualizamos la posición del mover
  mover.checkEdges();  // Verificamos si el mover ha tocado los bordes
  mover.show();        // Dibujamos el mover en el canvas
}

class Mover {
  constructor() {
    // El objeto tiene dos vectores: posición y velocidad
    this.position = createVector(random(width), random(height));  // Posición inicial aleatoria
    this.velocity = createVector(random(-2, 2), random(-2, 2)); // Velocidad aleatoria
  }

  update() {
    // La posición cambia según la velocidad
    this.position.add(this.velocity);
  }

  show() {
    stroke(0);           // Dibuja el contorno en negro
    strokeWeight(2);     // El grosor del contorno es 2
    fill(127);           // Color de relleno gris
    circle(this.position.x, this.position.y, 48);  // Dibuja un círculo en la posición del mover
  }

  checkEdges() {
    // Si el objeto toca los bordes, se reposiciona en el lado opuesto y cambia su velocidad aleatoriamente
    if (this.position.x > width || this.position.x < 0) {
      this.velocity.x = random(-2, 2);  // Cambio aleatorio en la velocidad X
    }

    if (this.position.y > height || this.position.y < 0) {
      this.velocity.y = random(-2, 2);  // Cambio aleatorio en la velocidad Y
    }
  }
}

Solución

Retroalimentación

Actividad 09

Experimentando con la aceleración

Enunciado: en el libro proponen una regla (que eventualmente se rompe cuando conviene :)):

The goal for programming motion is to come up with an algorithm for calculating acceleration and then let the trickle-down effect work its magic.

Para investigador el significado de esta frase te propone que construyas un experimento donde analices cómo se comporta un objeto en movimiento con:

• Aceleración constante.
• Aceleración aleatoria.
• Aceleración hacia el mouse.

Entrega:

• Reporta que encontraste para cada una de las posibles aceleraciones
• ¿Por qué?

🚀 Tu solución:

Estudiante

Con la constante el objeto simplemente sigue aumentando su velocidad hasta hacer que el programa falle.

let x = 0;
let v = 0;
let a = 0.1;

function setup() {
  createCanvas(600, 400);
  frameRate(60);
}

function draw() {
  background(255);

  v += a;

  x += v;

  if (x > width) {
    x = 0;
  }

  fill(0);
  ellipse(x, height / 2, 50, 50);

  fill(0);
  textSize(16);
  text("Velocidad: " + v.toFixed(2), 10, 30);
  text("Aceleración: " + a, 10, 50);
}

Con aceleración aleatoria tenia valores entre -0.1 y 0.1 me di cuenta que habia una tendencia de avanzar hacia adelante.

let x = 0;
let v = 0;
let a = 0;

function setup() {
  createCanvas(600, 400);
  frameRate(60);
}

function draw() {
  background(255);

  // Cambiar la aceleración aleatoriamente en cada fotograma
  a = random(-0.1, 0.1);   // Aceleración aleatoria entre -0.1 y 0.1

  v += a;

  x += v;

  if (x > width) {
    x = 0; // Resetea la posición a la izquierda
  }

  if (x < 0) {
    x = width; // Resetea la posición a la derecha
  }

  fill(0);
  ellipse(x, height / 2, 50, 50);

  fill(0);
  textSize(16);
  text("Velocidad: " + v.toFixed(2), 10, 30);
  text("Aceleración: " + a.toFixed(3), 10, 50);
}

Con aceleracón hacia el mouse

let x = 0;          // Posición inicial en el eje X
let v = 0;          // Velocidad inicial
let a = 0;          // Aceleración inicial

function setup() {
  createCanvas(600, 400);   // Crear el lienzo
  frameRate(60);            // Establecer la tasa de fotogramas
}

function draw() {
  background(255);          // Limpiar el lienzo en cada fotograma

  // Calcular la diferencia entre la posición del mouse y el objeto
  let distance = mouseX - x;

  // La aceleración será proporcional a la distancia entre el objeto y el mouse
  // Ajustar la constante de proporcionalidad para controlar la velocidad de respuesta
  a = distance * 0.001;  // Multiplicamos por un factor para controlar la aceleración

  // Actualizar la velocidad (v = v + a)
  v += a;

  // Actualizar la posición (x = x + v)
  x += v;

  // Si el objeto sale por el borde derecho, hacer que reaparezca a la izquierda
  if (x > width) {
    x = 0; // Resetea la posición a la izquierda
  }

  // Si el objeto sale por el borde izquierdo, hacer que reaparezca a la derecha
  if (x < 0) {
    x = width; // Resetea la posición a la derecha
  }

  // Dibujar el objeto (una pelota)
  fill(0);
  ellipse(x, height / 2, 50, 50);  // Dibujar la pelota en la posición x

  // Mostrar la velocidad y la aceleración
  fill(0);
  textSize(16);
  text("Velocidad: " + v.toFixed(2), 10, 30);
  text("Aceleración: " + a.toFixed(3), 10, 50);
}

Solución

Retroalimentación

Aplicación

En esta fase, aplicarás tus conocimientos sobre vectores para crear arte generativo algorítmico. Pondrás en práctica los conceptos aprendidos en las fases anteriores.

Actividad 10

Diseño: exploración de la idea

Enunciado: diseña una aplicación interactiva en tiempo que utilice los conceptos que investigaste. La aplicación debe:

• Generar una pieza de arte generativo algorítmico.
• Debes aplicar el marco MOTION 101.
• El contenido generado debe ser interactivo. Puedes utilizar mouse, teclado, cámara, micrófono, etc, para variar los parámetros del algoritmo en tiempo real.

Entrega:

• Un texto donde expliques tu intención de diseño.
• ¿Cómo piensas aplicar el marco MOTION 101 y por qué estos?
• Reporta los referentes que usaste para inspirarte.

🚀 Tu solución:

Estudiante

La idea es crear un objeto que se mueva con una aceleración constante hacia el mouse permitiendole cambiar la direccion segun donde esta el cursor y de tamaño con el teclado

Motion 101? basicamente implemente la aceleración constante que investigue en la actividad anterior para poder hacer el ejercicio.

Solución

Retroalimentación

Actividad 11

Materialización

Enunciado: vas a implementar tu aplicación diseñada.

Entrega:

• Código de la aplicación.
• Captura del contenido generado.
• En caso de realizar alguna variación al concepto original, escribe un texto donde expliques la razón del cambio.

🚀 Tu solución:

Estudiante

let x, y;
let vx = 0;
let vy = 0;
let ax = 0;
let ay = 0;
let mode = 'towardsMouse'; // Inicialmente aceleración hacia el mouse

// Tamaño inicial del objeto en movimiento
let objSize = 30;

// Array para almacenar las partículas
let particles = [];

function setup() {
  createCanvas(windowWidth, windowHeight);
  x = width / 2;
  y = height / 2;
}

function draw() {
  // Fondo blanco, no transparente para que las partículas se queden visibles
  background(255);

  // Calcular la distancia entre el objeto y el cursor
  let distToCursor = dist(x, y, mouseX, mouseY);

  // Ajustar la aceleración en función de la distancia
  let maxAccel = 0.1;  // Aceleración máxima
  let minAccel = 0.01; // Aceleración mínima
  let accelFactor = map(distToCursor, 0, width, minAccel, maxAccel);  // Mapeo de la distancia a la aceleración

  // Calcular el ángulo hacia el mouse
  let angle = atan2(mouseY - y, mouseX - x);

  // Aceleración hacia el mouse con la aceleración ajustada
  ax = cos(angle) * accelFactor;
  ay = sin(angle) * accelFactor;

  // Actualizar la velocidad y posición
  vx += ax;
  vy += ay;
  x += vx;
  y += vy;

  // Verificar si el objeto sale del canvas y hacer que aparezca en el lado opuesto
  if (x > width) {
    x = 0;  // Aparece por el lado izquierdo
  } else if (x < 0) {
    x = width;  // Aparece por el lado derecho
  }

  if (y > height) {
    y = 0;  // Aparece en la parte superior
  } else if (y < 0) {
    y = height;  // Aparece en la parte inferior
  }

  // Crear partículas con un tamaño relativo al tamaño del objeto
  let particleSize = objSize / 3;  // Las partículas son más pequeñas que el objeto
  particles.push(new Particle(x, y, particleSize));

  // Limitar el número de partículas para no sobrecargar la memoria
  if (particles.length > 1000) {
    particles.splice(0, 1);  // Elimina las partículas más antiguas
  }

  // Dibujar todas las partículas
  for (let i = 0; i < particles.length; i++) {
    particles[i].display();
  }

  // Mostrar la posición del objeto como un círculo
  fill(0);
  noStroke();
  ellipse(x, y, objSize, objSize);  // Usar objSize para el tamaño del objeto

  // Mostrar el texto indicando el modo actual
  fill(0);
  textSize(24);
  textAlign(CENTER);
  text("" + mode, width / 2, 30);
}

// Función para resetear la posición con el teclado
function keyPressed() {
  if (key === 'r' || key === 'R') {
    x = width / 2;
    y = height / 2;
    vx = 0;
    vy = 0;
  }

  // Cambiar el tamaño del objeto al presionar 'w' o 's'
  if (key === 'w' || key === 'W') {
    objSize += 5;  // Incrementar el tamaño
  }
  if (key === 's' || key === 'S') {
    objSize = max(5, objSize - 5);  // Reducir el tamaño sin permitir que sea menor a 5
  }
}

// Clase de partículas
class Particle {
  constructor(x, y, size) {
    this.x = x;
    this.y = y;
    this.size = size; // El tamaño de la partícula ahora se pasa como parámetro
    this.color = color(random(255), random(255), random(255)); // Color aleatorio
  }

  // Muestra la partícula
  display() {
    fill(this.color);  // Mantiene el color de la partícula
    noStroke();
    ellipse(this.x, this.y, this.size, this.size);  // Dibuja la partícula con el tamaño asignado
  }
}

Solución

Retroalimentación

Consolidación y matacognión

En esta fase final, reflexionarás sobre tu proceso de aprendizaje. Analizarás tus logros, identificarás áreas de mejora y consolidarás tu comprensión de los vectores y su aplicación.

Actividad 12

Análisis de resultados

Enunciado: revisa los resultados de las actividades de la fase APPLY. ¿Qué desafíos encontraste al aplicar los conceptos aprendidos? ¿Qué aprendiste de estos desafíos?

Entrega: descripción de los desafíos encontrados y las lecciones aprendidas durante la fase APPLY.

🚀 Tu solución:

Estudiante

Las actividades que más problema me dieron fueron las 5 y 6 debido a que me costo entender el funcionamiento de los vectores en movimiento a la hora de programarlos y que hicieran el movimiento deseado.

De ahí en más trabaje de forma constante logrande terminar la actividad 10 y 11 facilmente.

Solución

Retroalimentación

Actividad 13

Conexión con Diseño de Entretenimiento Digital

Enunciado: describe cómo los conceptos de esta unidad pueden ser utilizados en el diseño de videojuegos, experiencias interactivas o animaciones. Da ejemplos concretos.

Entrega: descripción de al menos tres aplicaciones de los conceptos aprendidos en el diseño de entretenimiento digital, con ejemplos concretos.

🚀 Tu solución:

Estudiante

¿Cómo funcionan los vectores en los videojuegos?

• Movimiento: Los vectores representan la dirección y la velocidad de un objeto. Imagina un personaje que camina en un videojuego. Su movimiento se puede representar con un vector que indica hacia dónde se dirige y qué tan rápido va.
• Fuerza y gravedad: En juegos con física, los vectores son esenciales para simular fuerzas como la gravedad, la fricción y la colisión. Por ejemplo, cuando un personaje salta, un vector de fuerza hacia arriba lo impulsa, y luego la gravedad lo atrae hacia abajo.
• Dirección de la cámara: Los vectores también se utilizan para controlar la dirección de la cámara en los juegos. Si estás jugando un juego de plataformas, la cámara se moverá con el personaje usando vectores para determinar su posición y ángulo.
• Efectos especiales: Los vectores pueden crear efectos visuales interesantes, como partículas que se mueven en diferentes direcciones o explosiones que se expanden.

Ejemplos específicos:

• Super Mario Bros: Cuando Mario salta, un vector de fuerza lo impulsa hacia arriba, y luego la gravedad lo atrae hacia abajo. La dirección del vector de fuerza determina la distancia y la altura del salto.
• Angry Birds: Los vectores se utilizan para calcular la trayectoria de los pájaros que lanzas. La fuerza y el ángulo del lanzamiento se representan con vectores que determinan la trayectoria del pájaro.
• Grand Theft Auto V: La dirección del vehículo y su velocidad se representan con vectores. Cuando el jugador acelera o gira, los vectores se actualizan para reflejar los cambios en el movimiento.

Solución

Retroalimentación

Actividad 14

Reflexión sobre el proceso de aprendizaje

Enunciado: reflexiona sobre tu propio proceso de aprendizaje durante esta unidad. ¿Qué estrategias te resultaron más efectivas para comprender los conceptos? ¿Qué podrías mejorar en futuras unidades?

Entrega:

• Descripción de las estrategias de aprendizaje utilizadas y su efectividad.
• Planteamiento de mejoras para futuras unidades.

🚀 Tu solución:

Estudiante

Basicamente trate de entendender y aplicar los conceptos al leerlos en los ejemplos y actividades, en ocaciones me tuve que ayudar con inteligencias artificiales como CHATGPT y ARIA para solucionar algunas actividades en las que me vi atascado

Experimentación:

• Simulaciones: Programas de simulación para experimentar con vectores. Cambiar la dirección, la magnitud y la posición de los vectores y observar cómo se comportan.

Ejercicios prácticos:

• Resuelve problemas: Buscar problemas que permitan aplicar los conceptos de vectores. Por ejemplo, puede calcular la resultante de dos vectores o la velocidad de un objeto en movimiento.

Solución

Retroalimentación

Actividad 15

Autoevaluación

Enunciado: evalúa tu nivel de comprensión de los conceptos de la unidad en una escala del 1 al 5 (1: Nada de comprensión, 5: Dominio completo). Justifica tu autoevaluación con ejemplos concretos de tu trabajo en la unidad. Identifica áreas donde necesitas reforzar tu aprendizaje.

Entrega:

• Autoevaluación con justificación y ejemplos concretos de tu trabajo que sustenten.
• Identificación de áreas de mejora.

🚀 Tu solución:

Estudiante

Nota 4.5

** La razón es que en dos de las actividades me tarde mucho debido a que me costo comprender como necesitaba que los vectores se trazaran y comportaran en ese ejercicio, pero a partir de ahi el entendimiebnt0 fue bueno y fluido

Solución

Retroalimentación