Unidad 4
Introducción
En las unidades anteriores has explorado el movimiento con el marco motion 101 manipulando la posición de los elementos gráficos de la simulación. En esta unidad explorarás el movimiento angular u oscilatorio.
¿Qué aprenderás en esta unidad?
En esta fase te mostraré algunos referentes que aplican los conceptos que investigarás y aplicarás en esta unidad.
Actividad 01
Te presente a Memo Akten
Enunciado: en esta actividad te presentaré a Memo Akten, un artista y programador que ha explorado las posibilidades de la inteligencia artificial en la creación de arte. Te voy a presentar una obra de Memo bajo el título sombrilla de Simple Harmonic Motion.
Entrega: escribe un párrafo en el que describas tu impresión sobre la obra de Memo Akten. ¿Qué te pareció? ¿Qué te llamó la atención? ¿Qué te gustó? ¿Qué no te gustó? ¿Qué te gustaría saber más?
Solo para los curiosos: dale una mirada a la obra Superradiance. Te dejo por aquí un video reciente: SUPERRADIANCE. Chapters 1-2. Short (Performance) version. By Memo Akten & Katie Peyton Hofstadter. Youtube.
🚀 Tu solución:
¿Qué te pareció?
WOW, que man tan teso
¿Qué te llamó la atención?
Las texturas y cómo se ve todo lo que hace. Visualmente es demasiado atractivo; me encantan los colores y los efectos visuales, como en la pieza donde uno podía pintar. ¿Quién no se siente atraído por eso? Me hace preguntarme cómo creó todo esto, especialmente considerando los conceptos que hemos visto.
Me llamó la atención cómo las formas y patrones emergen a partir de principios matemáticos, generando una sensación de fluidez y ritmo que se asemeja a fenómenos naturales. Me gustó especialmente la manera en que combina arte y ciencia para crear algo estéticamente atractivo y a la vez fundamentado en reglas físicas.
¿Qué te gustó?
- waves 2015
- The awesome machinery of Nature: We are all conncted(2021): me intrigo demasiado el nombre
- Reincarnation(2009)
- Body paint(2009): La mejor de todas
- Laser fingers(2013)
- Learning to see - Gloomy Sunday(2017):
¿Qué no te gustó?
las simulaciones como que eran infinitas que se iban como adentrando, me parecia que me mareaba y era demasiado visulemnte
- PixlFlippr(2021)
- All watched over By machines of Loving Grace (2021): Es demasiado
Investigación
Ahora vas a investigar algunos conceptos fundamentales que te servirán para diseñar tu aplicación en la fase que sigue.
Actividad 02
Conceptos fundamentales
Enunciado: analiza las siguientes simulaciones y responde las preguntas.
Te voy a proponer un par de simulaciones para que analices.
Primero mira esta simulación para el manejo de ángulos.
- ¿Qué está pasando en esta simulación? ¿Cuál es la interacción?
- Nota que en cada frame se está trasladando el origen del sistema de coordenadas al centro de la pantalla. ¿Por qué crees que se hace esto?
- Cuál es la relación entre el sistema de coordenadas y la función
rotate().
Nota esta parte del código:
line(-50, 0, 50, 0); stroke(0); strokeWeight(2); fill(127); circle(50, 0, 16); circle(-50, 0, 16);Observa que al dibujar los elementos gráficos parece que se está dibujando en la posición (0, 0) del sistema de coordenadas. ¿Por qué crees que se hace esto? y ¿Por qué aunque en cada frame se hace lo mismo, los elementos gráficos rotan?
Ahora analiza una simulación que muestra cómo puedes hacer para que los elementos gráficos de la simulación apunten en la dirección del movimiento.
- Identifica el marco motion 101. ¿Qué es lo que se está haciendo en este marco?
Observa detenidamente este fragmento de código de la simulación:
display() { let angle = this.velocity.heading();
stroke(0); strokeWeight(2); fill(127); push(); rectMode(CENTER); translate(this.position.x, this.position.y); rotate(angle); rect(0, 0, 30, 10);
pop(); }- ¿Qué hace la función
heading()? - ¿Qué hace la función
push()ypop()? Realiza algunos experimentos para entender su funcionamiento. - ¿Qué hace rectMode(CENTER)? Realiza algunos experimentos para entender su funcionamiento.
- ¿Cuál es la relación entre el ángulo de rotación y el vector de velocidad? Trata de dibujar en un papel el vector de velocidad y cómo se relaciona con el ángulo de rotación y la operación de traslación y rotación.
Entrega: reporta la respuesta a las preguntas anteriores.
🚀 Tu solución:
¿Qué está pasando en esta simulación? ¿Cuál es la interacción?
En esta simulación, se dibuja una linea con dos círculos en sus extremos. El centro de la linea está en el centro de la pantalla. La interacción ocurre cuando se presiona una tecla, lo que hace que el ángulo de rotación aumente, girando la figura alrededor de su centro.
Se traslada el origen al centro de la pantalla para que la rotación ocurra alrededor de ese punto
Se traslada el origen al centro de la pantalla para que la rotación ocurra alrededor de ese punto.
¿Cuál es la relación entre el sistema de coordenadas y la función rotate()?
La función rotate(angle) gira el sistema de coordenadas en torno a su origen actual. Como en la simulación se usa translate(width / 2, height / 2), el origen se mueve al centro de la pantalla, y la rotación ocurre en torno a ese punto. Si translate() no estuviera, la rotación se realizaría en la esquina superior izquierda de la pantalla (0,0), lo que generaría un movimiento diferente.
¿Por qué crees que se hace esto? y ¿Por qué aunque en cada frame se hace lo mismo, los elementos gráficos rotan?
Se dibujan los elementos con coordenadas relativas a (0,0) porque el sistema de coordenadas se traslada al centro de la pantalla con translate(width / 2, height / 2), haciendo que todo se posicione respecto a ese punto.
Los elementos rotan porque rotate(angle) gira todo el sistema de coordenadas antes de dibujar. Como angle aumenta al presionar una tecla, el sistema se inclina más en cada frame, haciendo que las figuras parezcan girar alrededor del centro. Sin rotate(), los elementos quedarían fijos en su orientación.
Identifica el marco motion 101. ¿Qué es lo que se está haciendo en este marco?
this.velocity.add(this.acceleration); this.velocity.limit(this.topspeed); this.position.add(this.velocity);En este código, un objeto se mueve en dirección al mouse aplicando una aceleración que lo empuja hacia él. La velocidad se actualiza en cada frame y se limita a un valor máximo (topspeed), lo que simula un movimiento más natural y progresivo. Además, el objeto reaparece en el lado opuesto de la pantalla cuando llega a los bordes, creando un efecto de movimiento continuo.
Análisis del código en display()
¿Qué hace la función heading()?
La función heading() obtiene el ángulo de dirección del vector de velocidad en radianes. Esto es útil para alinear visualmente el objeto en la misma dirección en la que se mueve.
¿Qué hacen push() y pop()?
push() guarda el estado actual de transformación del sistema de coordenadas (posición, rotación, escalado, etc.). pop() restaura el estado guardado antes de la transformación, evitando que afecte otros elementos en el lienzo. Esto es importante porque translate() y rotate() modifican el sistema de coordenadas, y sin push() y pop(), afectarían todo lo que se dibuje después.
¿Qué hace rectMode(CENTER)?
Esta función cambia el punto de referencia de los rectángulos. En modo CENTER, el rectángulo se dibuja desde su centro en lugar de su esquina superior izquierda. Esto facilita alinearlo con la rotación del objeto.
Relación entre el ángulo de rotación y el vector de velocidad
El ángulo de rotación (angle) se obtiene de la dirección del vector de velocidad (velocity.heading()). Como rotate(angle) gira el sistema de coordenadas, el rectángulo se orienta en la dirección en la que se mueve el objeto.
Actividad 03
Practica un poco
Enunciado: ahora es momento de practicar los conceptos anterior. Crea una simulación de un vehículo que puedas conducir por la pantalla utilizando las teclas de flecha: la flecha izquierda acelera el vehículo hacia la izquierda, y la flecha derecha acelera hacia la derecha. El vehículo tendrá forma triangular y debe apuntar en la dirección en la que se está moviendo actualmente.
Entrega:
- Enlace a la simulación en el editor de p5.js.
- Código de la simulación.
- Captura de pantalla de la simulación.
🚀 Tu solución:
// Simulación de un vehículo que se mueve con las flechas izquierda y derecha.
class Vehicle { constructor() { // Posición inicial en el centro de la pantalla this.position = createVector(width / 2, height / 2);
// Velocidad inicial en cero this.velocity = createVector(0, 0);
// Aceleración inicial en cero this.acceleration = createVector(0, 0);
// Máxima velocidad del vehículo this.topspeed = 4;
// Radio del vehículo this.r = 16; }
applyForce(force) { // Suma la fuerza a la aceleración this.acceleration.add(force); }
update() { // Agregamos la aceleración a la velocidad this.velocity.add(this.acceleration);
// Limitamos la velocidad para que no sea infinita this.velocity.limit(this.topspeed);
// Sumamos la velocidad a la posición this.position.add(this.velocity);
// Reiniciamos la aceleración para que no se acumule indefinidamente this.acceleration.mult(0); }
display() { // Calculamos el ángulo de rotación con base en la dirección del movimiento let angle = this.velocity.heading();
stroke(0); strokeWeight(2); fill(127);
// Guardamos el estado de la transformación push();
// Centramos el vehículo en su posición actual translate(this.position.x, this.position.y);
// Rotamos el vehículo en la dirección de su velocidad rotate(angle);
// Dibujamos un triángulo que representa al vehículo beginShape(); vertex(0, -this.r); // Punta del triángulo vertex(-this.r / 2, this.r); // Parte izquierda vertex(this.r / 2, this.r); // Parte derecha endShape(CLOSE);
// Restauramos el estado original de la transformación pop(); }}
let vehicle;
function setup() { createCanvas(640, 360); vehicle = new Vehicle();}
function draw() { background(255);
// Movimiento del vehículo con las teclas de flecha if (keyIsDown(LEFT_ARROW)) { vehicle.applyForce(createVector(-0.1, 0)); // Acelera hacia la izquierda } if (keyIsDown(RIGHT_ARROW)) { vehicle.applyForce(createVector(0.1, 0)); // Acelera hacia la derecha }
vehicle.update(); // Actualiza la posición y velocidad vehicle.display(); // Dibuja el vehículo}
Actividad 04
Relación con el marco motion 101
Enunciado: es momento de retomar lo que has aprendido en las unidades previas e integrarlo con los nuevos conceptos de esta unidad. Observa detenidamente la siguiente simulación: Motion 101 con fuerzas
- Identifica motion 101. ¿Qué modificación hay que hacer al motion 101 cuando se quiere agregar fuerzas acumulativas? Trata de recordar por qué es necesario hacer esta modificación.
- Identifica dónde está el Attractor en la simulación. Cambia el color de este.
- Observa que el Attractor tiene dos atributos this.dragging y this.rollover. Estos atributos no se modifican en el código, pero permitirían mover el attractor con el mouse y cambiar su color cuando el mouse está sobre él. ¿Cómo podrías modificar el código para que esto funcione? considera las funciones que ofrece p5.js para interactuar con el mouse.
Entrega: reporta la respuesta a las preguntas anteriores y los resultados de las modificaciones realizadas.
🚀 Tu solución:
Esta simulación representa un sistema donde múltiples objetos (Mover) son atraídos por un punto central (Attractor).
Cada objeto tiene masa, velocidad y aceleración, y responde a fuerzas externas.
1. Identificación de Motion 101
El Motion 101 es un marco conceptual que describe el movimiento de objetos en términos de posición, velocidad y aceleración. La idea clave es que:
La aceleración afecta la velocidad. La velocidad afecta la posición.
update() { this.velocity.add(this.acceleration); // La aceleración modifica la velocidad this.position.add(this.velocity); // La velocidad modifica la posición this.acceleration.mult(0); // Se reinicia la aceleración después de cada actualización}2. ¿Qué modificación hay que hacer para agregar fuerzas acumulativas?
En Motion 101 básico, la aceleración se establece directamente (por ejemplo, apuntando hacia el mouse). Sin embargo, si queremos agregar fuerzas acumulativas, en vez de reiniciar la aceleración cada cuadro, debemos permitir que las fuerzas se sumen con el tiempo.
La modificación clave está en cómo aplicamos la fuerza
applyForce(force) { let f = p5.Vector.div(force, this.mass); // F = ma (fuerza dividida por masa) this.acceleration.add(f); // Se acumulan fuerzas en cada cuadro}¿Por qué es necesario hacer esta modificación?
Porque en la vida real, los objetos no solo responden a una única fuerza en cada instante, sino que las fuerzas pueden acumularse. Por ejemplo, la gravedad y la resistencia del aire afectan un objeto al mismo tiempo.
3. Identificar el Attractor en la simulación
- El Attractor es el objeto que genera la fuerza de atracción para los Mover.
let attractor;attractor = new Attractor();- En la función draw(), el Attractor interactúa con cada Mover:
attractor.display(); // Dibuja el atractor
for (let i = 0; i < movers.length; i++) { let force = attractor.attract(movers[i]); // Calcula la fuerza de atracción movers[i].applyForce(force); // Aplica la fuerza al objeto
movers[i].update(); // Actualiza el movimiento del objeto movers[i].show(); // Dibuja el objeto}4. Cambio del color del Attractor
En la clase attractor cambiamos el color a morado
// Method to display display() { ellipseMode(CENTER); stroke(0); if (this.dragging) { fill(255,0,255); } else if (this.rollover) { fill(255,0,255); } else { fill(255,0,255); } ellipse(this.position.x, this.position.y, this.mass * 2); }}
Mover el attractor con el mouse y cambiar su color cuando el mouse está sobre él.
this.dragging: Es un booleano (valor true o false) que indica si el usuario está arrastrando el Attractor con el mouse.
- Cuando this.dragging = true, el Attractor sigue la posición del mouse.
- Cuando this.dragging = false, el Attractor permanece quieto.
this.rollover: También es un booleano (true o false), pero en este caso indica si el mouse está encima del Attractor.
- Cuando this.rollover = true, cambiamos el color del Attractor para indicar que podemos arrastrarlo.
- Cuando this.rollover = false, el Attractor vuelve a su color normal.
Para que funciones el ejercicio:
- mousePressed() → Detecta si el usuario hace clic sobre el Attractor.
- mouseReleased() → Suelta el Attractor cuando el usuario suelta el clic.
- mouseDragged() → Mueve el Attractor si está siendo arrastrado.
- Verificamos si el mouse está sobre el Attractor cambiando su color con rollover.
- debemos asegurarnos de que update() se llame dentro de draw() para que la detección de rollover y el arrastre funcionen correctamente.
let movers = [];let attractor; // Objeto atractor (atrae a los Movers)
function setup() { createCanvas(640, 240);
// Crear 20 objetos Mover con posición y masa aleatorias for (let i = 0; i < 20; i++) { movers.push(new Mover(random(width), random(height), random(0.1, 2))); }
attractor = new Attractor();// Crear el objeto Attractor}
function draw() { background(255);// ESTA PARTE attractor.update(); // ← Agrega esta línea para actualizar el atractor attractor.display();
for (let i = 0; i < movers.length; i++) { let force = attractor.attract(movers[i]); // Obtener la fuerza de atracción del atractor movers[i].applyForce(force);
movers[i].update(); movers[i].show(); }}- Cambio colores
// Genera fuerza gravitacionalclass Attractor { constructor() { this.position = createVector(width / 2, height / 2); this.mass = 20; // Masa del atractor (mayor que la de los Movers) this.G = 1;// Constante gravitacional this.dragging = false; // Indica si se está arrastrando this.rollover = false; // Indica si el mouse está encima this.offset = createVector(0, 0); // Compensa la posición al arrastrar }
// Método que genera la fuerza de atracción sobre un Mover attract(mover) { // Calculate direction of force let force = p5.Vector.sub(this.position, mover.position); // Distance between objects let distance = force.mag(); // Limiting the distance to eliminate "extreme" results for very close or very far objects distance = constrain(distance, 5, 25);
// Calculate gravitional force magnitude let strength = (this.G * this.mass * mover.mass) / (distance * distance); // Get force vector --> magnitude * direction force.setMag(strength); return force; }
//AGREGAMOS UN UPDATE update() { // Verificar si el mouse está sobre el Attractor let d = dist(mouseX, mouseY, this.position.x, this.position.y); this.rollover = d < this.mass; // Si está cerca, rollover es true
// Si se está arrastrando, actualiza la posición al mouse if (this.dragging) { this.position.x = mouseX + this.offset.x; this.position.y = mouseY + this.offset.y; } }
// Method to display display() { ellipseMode(CENTER); stroke(0);
if (this.dragging) { fill(150,0,0);// Rojo oscuro si se está arrastrando } else if (this.rollover) { fill(255,100,100); // Rojo claro si el mouse está encima } else { fill(255,0,0);// Rojo normal }
ellipse(this.position.x, this.position.y, this.mass * 2); }
}// Eventos del mouse (deben estar fuera de la clase)function mousePressed() { let d = dist(mouseX, mouseY, attractor.position.x, attractor.position.y); if (d < attractor.mass) { attractor.dragging = true; attractor.offset.x = attractor.position.x - mouseX; attractor.offset.y = attractor.position.y - mouseY; }} // FUNCIONES DEL MOUSEfunction mouseReleased() { attractor.dragging = false;}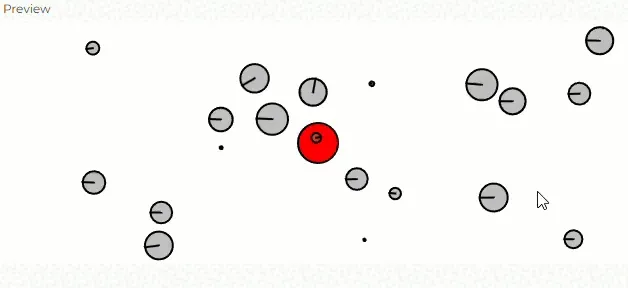
Actividad 05
Coordenadas polares
Enunciado: explora otro sistema de coordenadas útil cuando se trabaja con ángulos. Se trata de las coordenadas polares.
Considera esta simulación de coordenadas polares:
- Observa de nuevo esta parte del código ¿Cuál es la relación entre r y theta con las posiciones x y y? Puedes repasar entonces la definición de coordenadas polares y cómo se convierten a coordenadas cartesianas.
function draw() { background(255); // Translate the origin point to the center of the screen translate(width / 2, height / 2); // Convert polar to cartesian let x = r * cos(theta); let y = r * sin(theta); fill(127); stroke(0); strokeWeight(2); line(0, 0, x, y); circle(x, y, 48); theta += 0.02;}Modifica la función draw():
function draw() { background(255); // Translate the origin point to the center of the screen translate(width / 2, height / 2); let v = p5.Vector.fromAngle(theta); fill(127); stroke(0); strokeWeight(2); line(0, 0, x, y); circle(v.x, v.y, 48); theta += 0.02;}¿Qué ocurre? ¿Por qué?
Ahora realiza esta modificación:
function draw() { background(255); // Translate the origin point to the center of the screen translate(width / 2, height / 2); let v = p5.Vector.fromAngle(theta,r); fill(127); stroke(0); strokeWeight(2); line(0, 0, v.x, v.y); circle(v.x, v.y, 48); theta += 0.02;}- ¿Qué ocurre aquí? ¿Por qué?
Entrega: la respuesta a las preguntas anteriores.
🚀 Tu solución:
el sistema de coordenadas polares para mover un punto (representado por un círculo) alrededor del centro de la pantalla.
¿Cuál es la relación entre r y theta con las posiciones x y y?
a relación entre r y 𝜃 con las posiciones x e y y se basa en la conversión de coordenadas polares a cartesianas.
En coordenadas polares, la posición de un punto en un plano se determina por:
𝑟: La distancia desde el origen hasta el punto.
𝜃: El ángulo medido desde el eje positivo de las x, en radianes.La conversión a coordenadas cartesianas se realiza con las siguientes ecuaciones:
- x=rcos(θ) ----- x depende del radio y del coseno del ángulo 𝜃. A medida que 𝜃 cambia, el valor de 𝑥 oscila entre −𝑟 y +𝑟.
- y=rsin(θ) ----- y depende del radio y del seno del ángulo 𝜃. A medida que 𝜃 cambia, el valor de 𝑦 oscila entre −𝑟 y +𝑟.
Cada vez que se ejecuta draw(), el valor de theta aumenta en 0.02 radianes:
theta += 0.02;Esto provoca que el punto se mueva en un movimiento circular, ya que tanto 𝑥 como 𝑦 cambian continuamente en función del ángulo 𝜃.
- r determina el tamaño del círculo que sigue el punto.
- theta controla la rotación del punto alrededor del origen.
- x y y son las coordenadas cartesianas del punto en la circunferencia, obtenidas a partir de las funciones trigonométricas seno y coseno.
1. ¿Qué ocurre al ejecutar este código?
El punto ya no se mueve en un círculo grande como antes, sino que apenas se mueve en un círculo muy pequeño alrededor del origen. Esto se debe a que p5.Vector.fromAngle(theta) devuelve un vector unitario, es decir, un vector con magnitud 1, lo que significa que los valores de v.x y v.y siempre estarán en el rango de -1 a 1.
¿Cómo arreglarlo?
Podemos multiplicar el vector unitario por r para escalarlo al tamaño correcto.
p5.Vector.fromAngle(theta) solo da la dirección (con una magnitud de 1). Para que el punto se mueva en una circunferencia del mismo radio que antes, hay que multiplicar el vector por r.
1. ¿Qué ocurre al ejecutar este código?
En la línea circle(x, y, 48);, la variable y no está definida. En el código pasado, use let v = p5.Vector.fromAngle(theta, r);, lo que significa que ahora x y y están representados dentro del vector v. Por lo tanto, en la línea del círculo, en lugar de circle(x, y, 48);, debería ser circle(v.x, v.y, 48);.
¿Por qué ocurre esto?
- La función p5.Vector.fromAngle(theta, r) devuelve un vector con magnitud r y dirección theta. Esto significa que v.x y v.y ya incluyen la conversión de coordenadas polares a cartesianas, y no es necesario multiplicar por r después.
- p5.Vector.fromAngle(theta, r); ya se encarga de escalar el vector al tamaño correcto, por lo que la línea let v = p5.Vector.fromAngle(theta, r); genera un vector de longitud r, con las coordenadas ya calculadas correctamente.
Actividad 06
Funciones sinusoides
Enunciado: repasa la función sinusoide aquí.
- Recuerda estos conceptos: velocidad angular, frecuencia, periodo, amplitud y fase.
- Realiza una simulación en la que puedas modificar estos parámetros y observar cómo se comporta la función sinusoide.
Por ejemplo, te doy ideas, si juego solo con la fase, mira este ejemplo.
Entrega:
- Enlace a la simulación en el editor de p5.js.
- Código de la simulación.
- Captura de pantalla de la simulación.
🚀 Tu solución:
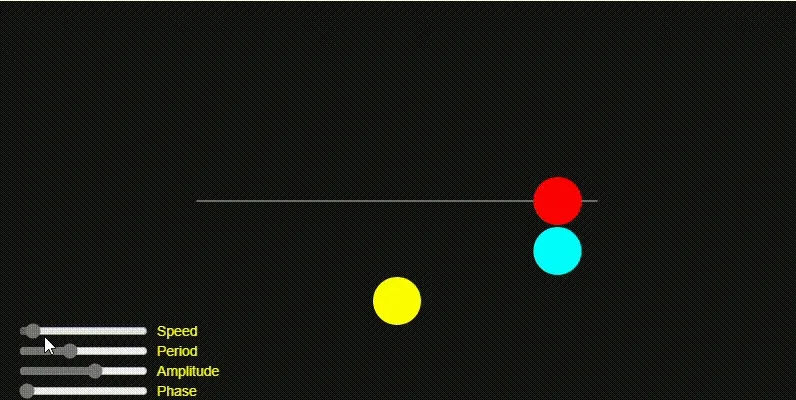
Función Sinusoide :atom:
let periodSlider, amplitudeSlider, phaseSlider, speedSlider;let phase = 0;let amplitude = 200;let period = 120;let speed = 0.02;
function setup() { createCanvas(800, 400);
// Crear sliders para controlar parámetros periodSlider = createSlider(10, 300, 120, 1); periodSlider.position(20, height - 60);
amplitudeSlider = createSlider(50, 300, 200, 1); amplitudeSlider.position(20, height - 40);
phaseSlider = createSlider(0, TWO_PI, 0, 0.05); phaseSlider.position(20, height - 20);
speedSlider = createSlider(0.01, 0.2, 0.02, 0.01); speedSlider.position(20, height - 80);
// Etiquetas de los sliders textSize(14); fill(255);}
function draw() { background(20);
text("Speed", 160, height - 65); text("Period", 160, height - 45); text("Amplitude", 160, height - 25); text("Phase", 160, height - 5);
// Leer valores de sliders period = periodSlider.value(); amplitude = amplitudeSlider.value(); phase = phaseSlider.value(); speed = speedSlider.value();
let x1 = amplitude * sin((TWO_PI * frameCount * speed) / period); let x2 = amplitude * sin((TWO_PI * frameCount * speed) / period + phase);
translate(width / 2, height / 2);
// Líneas de referencia stroke(200); line(-amplitude, 0, amplitude, 0);
// Dibujar círculos con colores brillantes let c1 = color(255, 0, 0); let c2 = color(0, 255, 255); let c3 = color(255, 255, 0);
noStroke(); fill(c1); circle(x1, 0, 48);
fill(c2); circle(x2, 50, 48);
fill(c3); circle(x1 - x2, 100, 48);}- Velocidad angular (speedSlider) → Controla qué tan rápido se mueve la onda.
- Período (periodSlider) → Define qué tan larga es la onda.
- Amplitud (amplitudeSlider) → Modifica qué tan grande es la oscilación.
- Fase (phaseSlider) → Cambia el desfase en tiempo real.
Actividad 07
Repasa conceptos de las unidades anteriores
Enunciado: aplica conceptos de la unidades anteriores tomando como base esta simulación. La idea es que la modifiques incluyendo un concepto de la unidad 1 (aleatoriedad) y la unidad 3 (fuerzas).
Entrega:
- Enlace a la simulación en el editor de p5.js.
- Código de la simulación.
- Captura de pantalla de la simulación.
🚀 Tu solución:
🏹 ¿Cómo funcionará?
- Flecha derecha (→): Aumenta la aceleración en X (empuja a la derecha).
- Flecha izquierda (←): Aumenta la aceleración en X en sentido contrario.
- Flecha arriba (↑): Aumenta la aceleración en Y (hacia arriba).
- Flecha abajo (↓): Aumenta la aceleración en Y (hacia abajo).
// Arreglo para almacenar los osciladoreslet oscillators = [];
// Color base para los osciladoreslet baseColor;
// Vector de aceleración constante (fuerza de viento) que afectará a los osciladoreslet wind;
function setup() { createCanvas(640, 360);
baseColor = color(50, 100, 200); // Define un color base azul oscuro
wind = createVector(0, 0); // Inicializa la aceleración del viento en (0,0), sin movimiento
// Crea 10 osciladores y los agrega al arreglo for (let i = 0; i < 10; i++) { oscillators.push(new Oscillator(i, 10)); }}
function draw() { background(240);
// Recorre el arreglo de osciladores y actualiza su movimiento for (let i = 0; i < oscillators.length; i++) { oscillators[i].applyForce(wind); // Aplica la fuerza del viento a cada oscilador oscillators[i].update(); // Actualiza su ángulo y velocidad oscillators[i].show(); // Dibuja el oscilador en pantalla }}
// Definimos la clase Oscillator para manejar el movimiento oscilatorioclass Oscillator { constructor(index, total) { // Crea un vector de ángulos inicial con valores aleatorios entre 0 y 2*PI this.angle = createVector(random(TWO_PI), random(TWO_PI));
// Crea una velocidad inicial para cada oscilador con valores pequeños aleatorios this.angleVelocity = createVector(random(-0.05, 0.05), random(-0.05, 0.05));
// Inicialmente, la aceleración del ángulo es cero this.angleAcceleration = createVector(0, 0);
// Define la amplitud del movimiento en X e Y de manera aleatoria this.amplitude = createVector( random(50, width / 2), random(50, height / 2) );
// Calcula un color basado en el índice del oscilador let factor = map(index, 0, total, 0.3, 1); // Ajusta el brillo de menor a mayor this.color = lerpColor(baseColor, color(255), factor); // Mezcla entre azul y blanco }
// Aplica una fuerza al oscilador (modifica su aceleración) applyForce(force) { this.angleAcceleration.add(force); }
// Actualiza el estado del oscilador en cada frame update() { this.angleVelocity.add(this.angleAcceleration); // La aceleración afecta la velocidad this.angle.add(this.angleVelocity); // La velocidad cambia el ángulo (movimiento) this.angleVelocity.limit(0.1); // Limita la velocidad para evitar movimientos exagerados this.angleAcceleration.mult(0); // Resetea la aceleración después de aplicarla }
// Dibuja el oscilador en pantalla show() { // Calcula la posición en la que debe estar el círculo usando funciones seno let x = sin(this.angle.x) * this.amplitude.x; let y = sin(this.angle.y) * this.amplitude.y;
push(); // Guarda la configuración actual de dibujo translate(width / 2, height / 2); // Mueve el punto de origen al centro del canvas stroke(0); // Define el color del borde como negro strokeWeight(2); // Grosor de la línea fill(this.color); // Rellena el círculo con su color asignado
// Dibuja una línea desde el centro (0,0) hasta la posición (x, y) line(0, 0, x, y);
// Dibuja un círculo en la posición (x, y) con un tamaño de 20 píxeles circle(x, y, 20);
pop(); // Restaura la configuración anterior del dibujo }}
// Función para detectar cuando se presiona una teclafunction keyPressed() { if (keyCode === RIGHT_ARROW) { wind.x += 0.002; // Aumenta la fuerza del viento hacia la derecha } else if (keyCode === LEFT_ARROW) { wind.x -= 0.002; // Aumenta la fuerza del viento hacia la izquierda } else if (keyCode === UP_ARROW) { wind.y -= 0.002; // Aumenta la fuerza del viento hacia arriba } else if (keyCode === DOWN_ARROW) { wind.y += 0.002; // Aumenta la fuerza del viento hacia abajo }}📌 Conceptos de las Unidades Aplicado
- Unidad 1 (Aleatoriedad): Se usa random() para generar ángulos iniciales y amplitudes aleatorias, lo que hace que cada oscilador se mueva de manera única.
- Unidad 3 (Fuerzas): Se usa un vector de fuerza (wind) que afecta la aceleración de los osciladores.
- Física del Movimiento: Cada oscilador sigue una dinámica de movimiento oscilatorio, donde se aplican las ecuaciones de aceleración y velocidad.
- Aceleración Constante: fuerza con las teclas de flecha, el concepto de aplicar una fuerza externa sigue siendo clave.
Actividad 08
Ondas
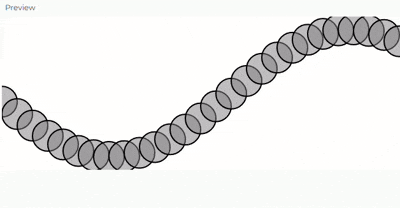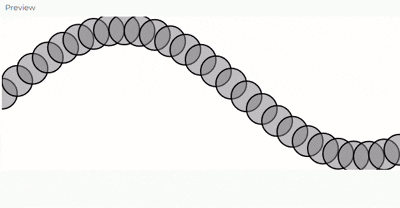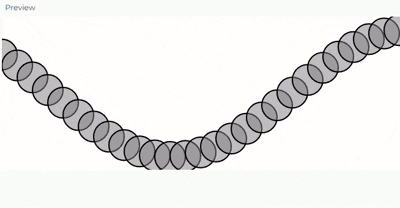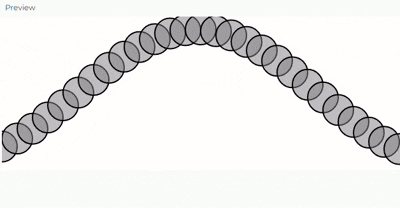
Enunciado: vas a observar este código que simula una onda.
El reto es que hagas que se esta onda se mueva como una ola.
Entrega:
- Enlace a la simulación en el editor de p5.js.
- Código de la simulación.
- Captura de pantalla de la simulación.
🚀 Tu solución:
Para hacer que la onda se mueva como una ola, actualizace el dibujo en cada fotograma en draw() en lugar de dibujar todo en setup(). Esto permitirá que la onda fluya y se vea animada.
// Variables para controlar la ondalet angle = 0;let angleVelocity = 0.2;let amplitude = 100;let xSpacing = 24; // Espaciado entre los puntos de la ondalet offset = 0; // Desplazamiento para que la onda se mueva
function setup() { createCanvas(640, 240);}
function draw() { background(255); stroke(0); strokeWeight(2); fill(127, 127);
let currentAngle = angle; // Reiniciamos el ángulo para cada onda
for (let x = 0; x <= width; x += xSpacing) { let y = amplitude * sin(currentAngle + offset); // Calcula la posición y circle(x, y + height / 2, 48); // Dibuja el círculo en la onda currentAngle += angleVelocity; // Aumentamos el ángulo para el siguiente punto }
offset += 0.1; // Hace que la onda fluya en el tiempo como una ola}- Se mueve la lógica de dibujo a draw() para que la animación sea continua.
- Se usa una variable offset para desplazar la onda horizontalmente con el tiempo, creando el efecto de movimiento de ola.
- Mantiene el cálculo de y con sin(), pero ahora le sumamos offset para el desplazamiento.
Actividad 09
Resortes
Enunciado: modifica esta simulación para crear un sistema de dos resortes conectados en serie.
Entrega:
- Enlace a la simulación en el editor de p5.js.
- Código de la simulación.
- Captura de pantalla de la simulación.
🚀 Tu solución:
Dos resortes conectados en serie.
- El primer resorte (spring1) sigue conectado a un punto de anclaje fijo
- La primera masa (bob1) conectada al primer resorte
- Un segundo resorte (spring2) que conecta la primera masa con una segunda masa
- La segunda masa (bob2) que cuelga del segundo resorte
Crear nuevos métodos en la clase Spring para permitir la conexión entre dos masas (no solo entre un anclaje fijo y una masa)
Metodos:
connectBobs(bob1, bob2) { // Vector que apunta desde bob1 hasta bob2 let force = p5.Vector.sub(bob2.position, bob1.position); // Calcular la distancia actual let currentLength = force.mag(); // El estiramiento es la diferencia entre la distancia actual y la longitud de reposo let stretch = currentLength - this.restLength;
// Calcular la magnitud de la fuerza let magnitude = -1 * this.k * stretch; force.setMag(magnitude);
// Aplicar la fuerza a ambas masas en direcciones opuestas bob1.applyForce(force.copy().mult(-1)); bob2.applyForce(force);}-
Calcula la fuerza del resorte basándose en la distancia entre dos masas (no entre un anclaje y una masa)
-
Aplica fuerzas iguales y opuestas a ambas masas (tercera ley de Newton)
-
constrainLengthBetweenBobs(bob1, bob2, minlen, maxlen): Mantiene la distancia entre las dos masas dentro de un rango específico, evitando que los resortes se estiren o compriman demasiado.
-
showLineBetweenBobs(bob1, bob2): Dibuja visualmente el resorte entre las dos masas.
Conexión de los resortes en el programa principal
// Conectar spring1 a bob1 (como en el código original)spring1.connect(bob1);
// Conectar bob1 y bob2 mediante spring2 (nuevo)spring2.connectBobs(bob1, bob2);Aplicación de fuerzas y restricciones
- Apliqué la gravedad a ambas masas:
javascriptCopiarlet gravity = createVector(0, 1);bob1.applyForce(gravity.copy().mult(bob1.mass));bob2.applyForce(gravity.copy().mult(bob2.mass));- Apliqué restricciones a ambos resortes:
javascriptCopiarspring1.constrainLength(bob1, 20, 300);spring2.constrainLengthBetweenBobs(bob1, bob2, 20, 300);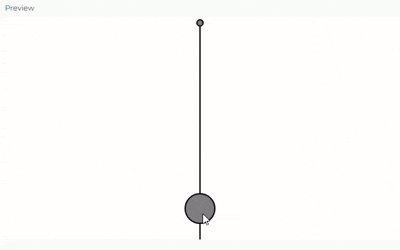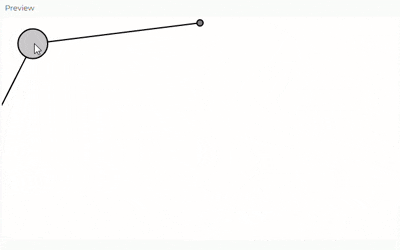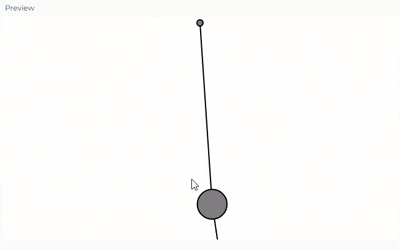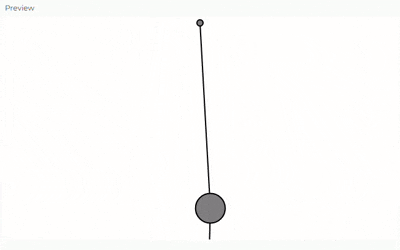
Actividad 10
Péndulos
Enunciado: modifica esta simulación para crear un sistema de dos péndulos conectados en serie.
Entrega:
- Enlace a la simulación en el editor de p5.js.
- Código de la simulación.
- Captura de pantalla de la simulación.
🚀 Tu solución:
Péndulo Doble 🐧
Clase DoblePendulum
El constructor inicializa todas las propiedades del doble péndulo, incluyendo la geometría (longitudes y ángulos), las propiedades físicas (masas y gravedad) y las variables para la interacción
class DoublePendulum { constructor(x, y, r1, r2) { // Propiedades iniciales this.pivot = createVector(x, y); // Punto de pivote fijo this.r1 = r1; // Longitud del primer péndulo this.r2 = r2; // Longitud del segundo péndulo this.angle1 = PI / 4; // Ángulo inicial del primer péndulo (45 grados) this.angle2 = PI / 2; // Ángulo inicial del segundo péndulo (90 grados) this.angleVelocity1 = 0.0; // Velocidad angular inicial del primer péndulo this.angleVelocity2 = 0.0; // Velocidad angular inicial del segundo péndulo this.angleAcceleration1 = 0.0; // Aceleración angular inicial del primer péndulo this.angleAcceleration2 = 0.0; // Aceleración angular inicial del segundo péndulo this.m1 = 10; // Masa del primer péndulo this.m2 = 10; // Masa del segundo péndulo this.g = 1; // Constante gravitacional
// Variables para la interacción del mouse this.dragging1 = false; // Si estamos arrastrando el primer péndulo this.dragging2 = false; // Si estamos arrastrando el segundo péndulo }
update() { // Si ninguno de los péndulos está siendo arrastrado, actualiza según la física if (!this.dragging1 && !this.dragging2) { // Ecuaciones diferenciales para el movimiento del doble péndulo let num1 = -this.g * (2 * this.m1 + this.m2) * sin(this.angle1); let num2 = -this.m2 * this.g * sin(this.angle1 - 2 * this.angle2); let num3 = -2 * sin(this.angle1 - this.angle2) * this.m2; let num4 = this.angleVelocity2 * this.angleVelocity2 * this.r2 + this.angleVelocity1 * this.angleVelocity1 * this.r1 * cos(this.angle1 - this.angle2); let den = this.r1 * (2 * this.m1 + this.m2 - this.m2 * cos(2 * this.angle1 - 2 * this.angle2)); this.angleAcceleration1 = (num1 + num2 + num3 * num4) / den;
let num5 = 2 * sin(this.angle1 - this.angle2); let num6 = this.angleVelocity1 * this.angleVelocity1 * this.r1 * (this.m1 + this.m2) + this.g * (this.m1 + this.m2) * cos(this.angle1) + this.angleVelocity2 * this.angleVelocity2 * this.r2 * this.m2 * cos(this.angle1 - this.angle2); let den2 = this.r2 * (2 * this.m1 + this.m2 - this.m2 * cos(2 * this.angle1 - 2 * this.angle2)); this.angleAcceleration2 = (num5 * num6) / den2;
// Actualizar velocidades con las aceleraciones calculadas this.angleVelocity1 += this.angleAcceleration1; this.angleVelocity2 += this.angleAcceleration2;
// Aplicar un poco de amortiguamiento (reduce la energía lentamente) this.angleVelocity1 *= 0.999; this.angleVelocity2 *= 0.999;
// Actualizar ángulos con las velocidades calculadas this.angle1 += this.angleVelocity1; this.angle2 += this.angleVelocity2; } }
calculatePositions() { //Convierte los ángulos en coordenadas cartesianas // Posición de la primera masa this.x1 = this.r1 * sin(this.angle1) + this.pivot.x; this.y1 = this.r1 * cos(this.angle1) + this.pivot.y;
// Posición de la segunda masa this.x2 = this.x1 + this.r2 * sin(this.angle2); this.y2 = this.y1 + this.r2 * cos(this.angle2); }
show() { this.calculatePositions();
stroke(0); strokeWeight(2); fill(127);
// Dibujar el primer péndulo line(this.pivot.x, this.pivot.y, this.x1, this.y1); circle(this.x1, this.y1, this.m1 * 2);
// Dibujar el segundo péndulo line(this.x1, this.y1, this.x2, this.y2); circle(this.x2, this.y2, this.m2 * 2); }
clicked(mx, my) { // detecta si el usuario ha hecho clic en alguna de las masas // Verificar primero la segunda masa (la que está encima visualmente) let d2 = dist(mx, my, this.x2, this.y2); if (d2 < this.m2) { this.dragging2 = true; // Reiniciar velocidades cuando se empieza a arrastrar this.angleVelocity1 = 0; this.angleVelocity2 = 0; return true; }
// Luego verificar la primera masa let d1 = dist(mx, my, this.x1, this.y1); if (d1 < this.m1) { this.dragging1 = true; // Reiniciar velocidades cuando se empieza a arrastrar this.angleVelocity1 = 0; this.angleVelocity2 = 0; return true; }
return false; }
stopDragging() { //desactiva ambas variables de arrastre cuando el usuario suelta el mouse. this.dragging1 = false; this.dragging2 = false; }
drag() { // actualiza los ángulos según la posición del mouse cuando se arrastra una masa if (this.dragging1) { // Calcular el nuevo ángulo basado en la posición del mouse let dx = mouseX - this.pivot.x; let dy = mouseY - this.pivot.y; this.angle1 = atan2(dx, dy);
// Actualizar la posición basada en el nuevo ángulo this.calculatePositions(); } else if (this.dragging2) { // Calcular el nuevo ángulo basado en la posición del mouse relativa a la primera masa let dx = mouseX - this.x1; let dy = mouseY - this.y1; this.angle2 = atan2(dx, dy);
// Actualizar la posición basada en el nuevo ángulo this.calculatePositions(); } }}
let doublePendulum;
function setup() { createCanvas(640, 480); // Crear un lienzo de 640x480 píxeles doublePendulum = new DoublePendulum(width / 2, 100, 125, 125); // Crear el doble péndulo}
function draw() { background(255); // Establecer fondo blanco
// Actualizar la física doublePendulum.update();
// Actualizar si se está arrastrando if (mouseIsPressed) { doublePendulum.drag(); }
// Mostrar el péndulo doublePendulum.show();}
function mousePressed() { doublePendulum.clicked(mouseX, mouseY); // Comprobar si se ha hecho clic en alguna masa}
function mouseReleased() { doublePendulum.stopDragging(); // Dejar de arrastrar cuando se suelta el mouse}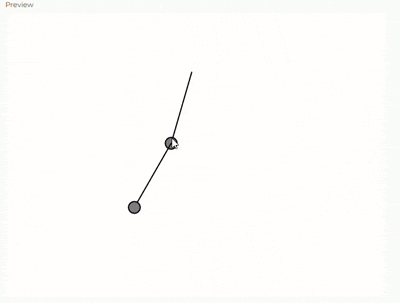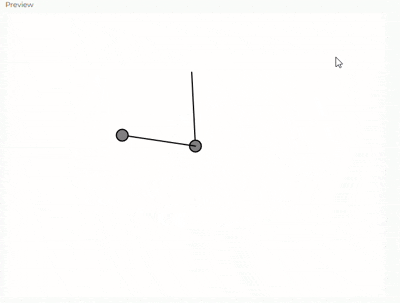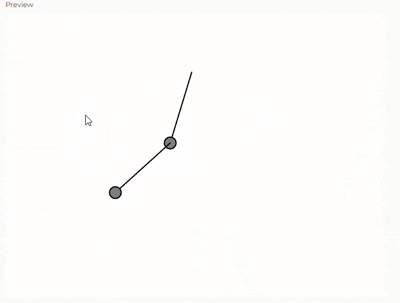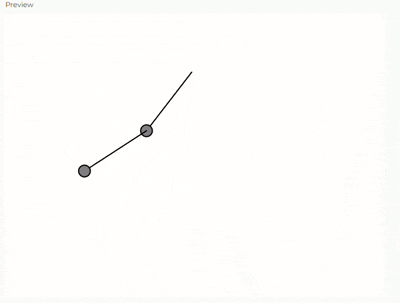
Aplicación
Es momento de aplicar los conceptos aprendidos en la unidad.
Actividad 11
Obra de arte generativa algorítmica interactiva en tiempo real
Enunciado: diseña e implementa una obra de arte generativa algorítmica interactiva en tiempo real en p5.js que cumpla con los siguientes requisitos:
- Selecciona uno de los conceptos con los que experimentaste en la fase de investigación y propón la obra alrededor de este.
- La obra debe ser interactiva en tiempo real. Puedes usar teclado, mouse, música, el micrófono, video, sensor o cualquier otro dispositivo de entrada.
- Documenta el proceso de creación, incluyendo la idea inicial, bocetos, experimentación con el código y el resultado final.
Entrega:
- Enlace a tu obra en el editor de p5.js.
- El código.
- Una captura de pantalla con una imagen de tu obra.
🚀 Tu solución:
1. Clase DoublePendulum
- Esta clase representa el doble péndulo y contiene toda la lógica para su simulación, dibujo y manejo de interacción.
2. Metodo Update
- cCalcula cómo se mueven los ángulos del doble péndulo usando fórmulas físicas basadas en las ecuaciones del movimiento.
- Si no sé esta arrastrando las masas (!this.dragging1 && !this.dragging2), se aplican las leyes de la dinámica al sistema.
3. Metodo Show
- dibuja las cuerdas, las masas y la traza que deja el movimiento del segundo péndulo.
4.Interacciones
- drag: Actualiza los ángulos si estás arrastrando una masa.
- clicked(mx, my): Detecta si hiciste clic cerca de una masa y activa el arrastre.
- stopDragging: Finaliza el arrastre cuando se suelta el mouse.
class DoublePendulum { constructor(x, y, r1, r2) { this.pivot = createVector(x, y); // Punto de pivote (la parte fija donde cuelga el péndulo). this.r1 = r1; // Longitud de la primera cuerda. this.r2 = r2; // Longitud de la segunda cuerda. this.angle1 = PI / 4; // Ángulo inicial del primer péndulo. this.angle2 = PI / 2; // Ángulo inicial del segundo péndulo. this.angleVelocity1 = 0.0; // Velocidad angular del primer péndulo. this.angleVelocity2 = 0.0; // Velocidad angular del segundo péndulo. this.angleAcceleration1 = 0.0; // Aceleración angular del primer péndulo. this.angleAcceleration2 = 0.0; // Aceleración angular del segundo péndulo. this.m1 = 10; // Masa del primer péndulo. this.m2 = 10; // Masa del segundo péndulo. this.g = 1; // Gravedad (puedes ajustarla para hacerlo más rápido o lento). this.dragging1 = false; // Indica si el primer péndulo está siendo arrastrado. this.dragging2 = false; // Indica si el segundo péndulo está siendo arrastrado. this.prevX2 = null; // Última posición en X del segundo péndulo (para la traza). this.prevY2 = null; // Última posición en Y del segundo péndulo (para la traza). this.trailColor = color(0, 255, 0, 150); // Color de la traza (verde semitransparente).}
update() { if (!this.dragging1 && !this.dragging2) { let num1 = -this.g * (2 * this.m1 + this.m2) * sin(this.angle1); let num2 = -this.m2 * this.g * sin(this.angle1 - 2 * this.angle2); let num3 = -2 * sin(this.angle1 - this.angle2) * this.m2; let num4 = this.angleVelocity2 ** 2 * this.r2 + this.angleVelocity1 ** 2 * this.r1 * cos(this.angle1 - this.angle2); let den = this.r1 * (2 * this.m1 + this.m2 - this.m2 * cos(2 * this.angle1 - 2 * this.angle2)); this.angleAcceleration1 = (num1 + num2 + num3 * num4) / den;
let num5 = 2 * sin(this.angle1 - this.angle2); let num6 = this.angleVelocity1 ** 2 * this.r1 * (this.m1 + this.m2) + this.g * (this.m1 + this.m2) * cos(this.angle1); let num7 = this.angleVelocity2 ** 2 * this.r2 * this.m2 * cos(this.angle1 - this.angle2); let den2 = this.r2 * (2 * this.m1 + this.m2 - this.m2 * cos(2 * this.angle1 - 2 * this.angle2)); this.angleAcceleration2 = (num5 * (num6 + num7)) / den2;
this.angleVelocity1 += this.angleAcceleration1; this.angleVelocity2 += this.angleAcceleration2; this.angle1 += this.angleVelocity1; this.angle2 += this.angleVelocity2; } }
show() { let x1 = this.pivot.x + this.r1 * sin(this.angle1); let y1 = this.pivot.y + this.r1 * cos(this.angle1); let x2 = x1 + this.r2 * sin(this.angle2); let y2 = y1 + this.r2 * cos(this.angle2);
stroke(255); strokeWeight(2); fill(255); line(this.pivot.x, this.pivot.y, x1, y1); line(x1, y1, x2, y2); ellipse(x1, y1, this.m1 * 2); ellipse(x2, y2, this.m2 * 2);
if (this.prevX2 !== null && this.prevY2 !== null) { trailGraphics.stroke(this.trailColor); trailGraphics.strokeWeight(2); trailGraphics.line(this.prevX2, this.prevY2, x2, y2); }
this.prevX2 = x2; this.prevY2 = y2; }
drag() { let x1 = this.pivot.x + this.r1 * sin(this.angle1); let y1 = this.pivot.y + this.r1 * cos(this.angle1); let x2 = x1 + this.r2 * sin(this.angle2); let y2 = y1 + this.r2 * cos(this.angle2);
if (this.dragging1) { this.angle1 = atan2(mouseY - this.pivot.y, mouseX - this.pivot.x) - PI / 2; this.angleVelocity1 = 0; } else if (this.dragging2) { this.angle2 = atan2(mouseY - y1, mouseX - x1) - PI / 2; this.angleVelocity2 = 0; } }
clicked(mx, my) { let x1 = this.pivot.x + this.r1 * sin(this.angle1); let y1 = this.pivot.y + this.r1 * cos(this.angle1); let x2 = x1 + this.r2 * sin(this.angle2); let y2 = y1 + this.r2 * cos(this.angle2);
// Hacer que las áreas de detección sean más grandes if (dist(mx, my, x1, y1) < this.m1 * 2) { this.dragging1 = true; } else if (dist(mx, my, x2, y2) < this.m2 * 2) { this.dragging2 = true; } }
stopDragging() { this.dragging1 = false; this.dragging2 = false; }}
let doublePendulum;let trailGraphics;
function setup() { createCanvas(640, 480); background(0); // Fondo negro trailGraphics = createGraphics(width, height); trailGraphics.background(0); trailGraphics.stroke(0, 255, 0, 150); // Color del trazo en verde trailGraphics.strokeWeight(2);
// Crear un péndulo doble doublePendulum = new DoublePendulum(width / 2, 200, 125, 125);}
function draw() { background(0); // Fondo negro image(trailGraphics, 0, 0); // Dibujar el rastro doublePendulum.update(); doublePendulum.show();}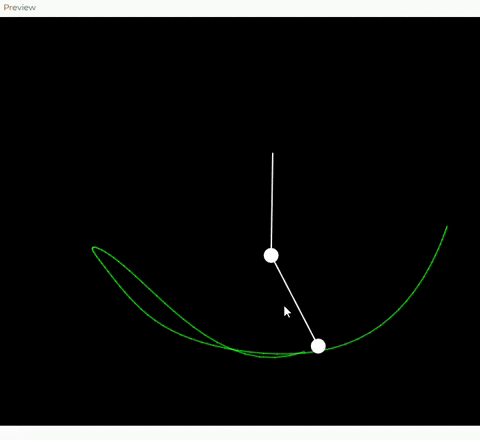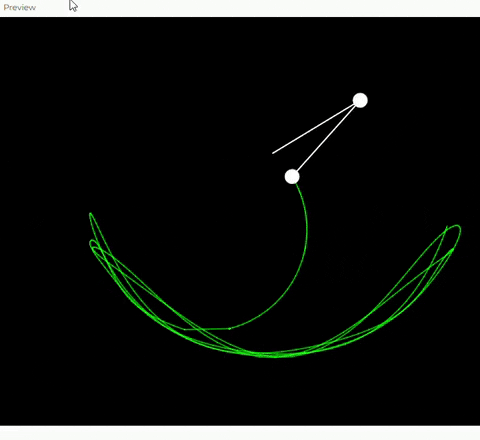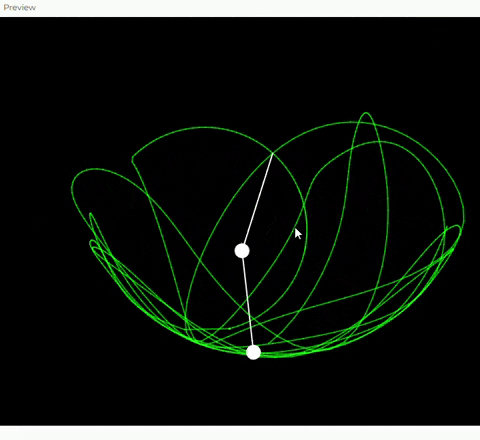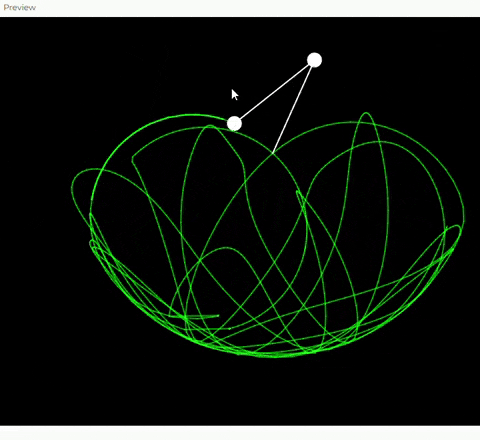
Consolidación y metacognición
He venido escuchando que esta es una fase de relleno 😭. Nada
más lejos de la verdad, de verdad. En esta fase del proceso de aprendizaje
es donde miras hacia atrás y consolidas lo que aprendiste. Adicionalmente,
reflexionas sobre tu proceso de aprendizaje y las posibilidades de aplicar lo
aprendido en otros contextos.
Actividad 12
Consolidación
Enunciado: analiza tu obra de arte generativa respondiendo las siguientes preguntas:
- ¿Qué concepto de oscilación utilizaste como base para tu obra? Describe cómo lo implementaste.
- ¿Cómo funciona la interacción en tu obra? Explica cómo el usuario puede modificar la obra en tiempo real.
- ¿Qué desafíos encontraste durante el proceso de creación? ¿Cómo los superaste?
- ¿Qué aprendiste sobre las oscilaciones y su aplicación en el arte generativo?
Entrega: responde a las preguntas.
🚀 Tu solución:
¿Qué concepto de oscilación utilizaste como base para tu obra? Describe cómo lo implementaste.
Utilice el concepto de oscilación no lineal a través del modelo de un doble péndulo, que es un sistema físico conocido por su comportamiento caótico y sus patrones complejos. Implementé este concepto mediante las ecuaciones de movimiento del doble péndulo, que consideran las fuerzas gravitacionales, las masas de los objetos y la interacción entre los ángulos de las oscilaciones.
El sistema calcula la aceleración, velocidad y posición de las dos masas en cada fotograma, utilizando fórmulas derivadas de las leyes de Newton. Esto nos permitió crear movimientos realistas y fascinantes, con trayectorias que reflejan movimientos imprecedibles y visualmente atractiva del caos.
2. ¿Cómo funciona la interacción en tu obra? Explica cómo el usuario puede modificar la obra en tiempo real.
La interacción en mi obra se basa en la capacidad del usuario para arrastrar las masas del péndulo y modificar su posición inicial. Cuando el usuario hace clic cerca de una de las masas y arrastra el mouse, el sistema actualiza los ángulos correspondientes para seguir la posición del cursor. Esto permite que el usuario altere el movimiento del péndulo y explore creando trayectorias y patrones únicos en tiempo real.
Además, cada modificación del usuario afecta directamente la traza que deja el segundo péndulo, haciendo visible cada trazo que da el pendulo.
3. ¿Qué desafíos encontraste durante el proceso de creación? ¿Cómo los superaste?
Uno de los mayores desafíos fue implementar las ecuaciones de movimiento de manera precisa, ya que son complejas y altamente sensibles a los parámetros iniciales. Tuve que asegurarme de que los cálculos matemáticos fueran consistentes y ajustados a las propiedades del sistema. Para superar esto, me base en el codigo anterior que hicimos sobre pendulos.
Otro desafío fue integrar la interacción del usuario sin que el sistema perdiera estabilidad.
4. ¿Qué aprendiste sobre las oscilaciones y su aplicación en el arte generativo?
Aprendí que las oscilaciones son una herramienta poderosa para crear patrones visuales complejos y dinámicos. En particular, las oscilaciones no lineales revelaron cómo el caos puede transformarse en arte generativo, produciendo resultados únicos que dependen tanto de las condiciones iniciales como de las interacciones humanas.
Actividad 13
Metacognición
Enunciado: reflexiona sobre tu propio proceso de aprendizaje en esta unidad.
- ¿Qué estrategias de aprendizaje utilizaste?
- ¿Qué te funcionó mejor para comprender los conceptos?
- ¿Qué podrías mejorar?
- ¿Cómo te sentiste durante el proceso de aprendizaje?
- ¿Qué te motivó?
- ¿Qué te frustró?
Entrega: respuesta a las preguntas.
🚀 Tu solución:
¿Qué estrategias de aprendizaje utilizaste?
Durante esta unidad, utilicé estrategias como la exploración práctica, la búsqueda activa de información y la resolución de problemas mediante ensayo y error mediante los ejercicios de clase.
¿Qué te funcionó mejor para comprender los conceptos?
Lo que mejor me funcionó fue aprender haciendo, es decir, experimentar directamente con el código y observar cómo los cambios en las ecuaciones y parámetros afectaban el comportamiento del doble péndulo. Visualizar los resultados en tiempo real me permitió comprender conceptos complejos, como el caos y las oscilaciones, de una forma más intuitiva.
¿Qué podrías mejorar?
Podría mejorar mi gestión del tiempo, ya que en algunos momentos me concentré demasiado en detalles específicos del código y dejé de lado otros aspectos importantes del proyecto.
¿Cómo te sentiste durante el proceso de aprendizaje?
Me sentí normal, pero un poco cansada pero me intereso, especialmente al ver cómo los conceptos abstractos cobraban vida en forma de patrones visuales. Sin embargo, también hubo momentos de frustración, especialmente cuando no lograba que el código funcionara como esperaba o cuando los errores no eran fáciles de identificar.
¿Qué te motivó?
Me motivó la idea de crear algo en donde el usuario pueda contrlar algo pero luegpo no, algo que por el movimiento forme unos trazos unicos y visualmente atractivo.
¿Qué te frustró?
Me frustró la complejidad de las ecuaciones y su sensibilidad a los parámetros iniciales, ya que pequeños errores podían hacer que todo el sistema se comportara de manera incorrecta. También fue un reto manejar la interacción en tiempo real sin que el sistema perdiera estabilidad.