Unidad 2
Introducción
En esta unidad, te sumergirás en el fascinante mundo de los vectores, las fuerzas invisibles que dan vida a tus creaciones digitales. Experimentarás con conceptos matemáticos y físicos, como velocidad y aceleración, para controlar el movimiento en tus proyectos interactivos. Aprenderás a manipular vectores en p5.js, pero recuerda que este conocimiento es aplicable a cualquier lenguaje de programación.
¿Qué aprenderás en esta unidad?
En esta fase, vas a revisar algunos conceptos básicos de vectores que ya conoces tu paso por ciencia básica.
Actividad 01
Analiza una aplicación interactiva
Enunciado: analiza el ejemple: Example 1.2: Bouncing Ball with Vectors!
- ¿Cómo funciona la suma dos vectores?
- ¿Por qué esta línea position = position + velocity; no funciona?
Entrega: escribe en tu bitácora la solución a las preguntas anteriores.
🚀 Tu solución:
Example 1.2: Bouncing Ball with Vectors!
¿Cómo funciona la suma dos vectores?
Cada vector tiene dos componentes, una x y una y. Para sumar los dos vectores, sume los componentes x y para crear un nuevo vector.
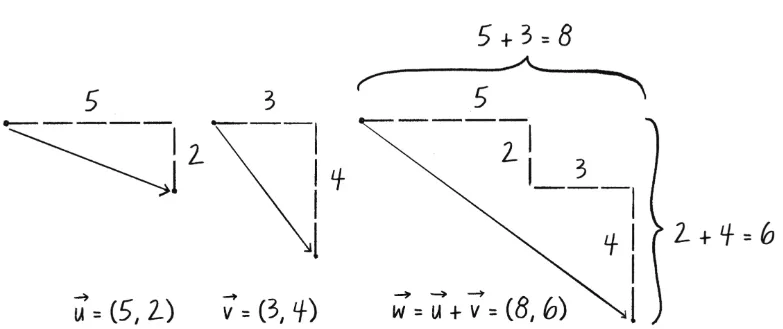
Propiedades de suma con vectores La suma con vectores sigue las mismas reglas algebraicas que con los números reales.
- Conmutativo: 3+2=2+3
- Asociativo: (3+2)+1=3+(2+1)
En p5.js se usa
Vectoradd()VectorLa función busca los componentes x e y de los dos vectores y los suma por separado.
class Vector {
constructor(x, y) { this.x = x; this.y = y; }//Una función para agregar otro vector a este vector. Agregue los componentes x y los componentes y por separado. add(v) { this.x = this.x + v.x; this.y = this.y + v.y; }}¿Por qué esta línea position = position + velocity; no funciona?
No funciona porque está intentando sumar dos vectores, pero los vectores necesitan sumarse componente por componente.
Se debe utilizar, ya que suma la velocidad a la posición.
position.add(velocity);Ejemplo: Si tengo una posición position = (x, y) y una velocidad velocity = (xspeed, yspeed), para sumarlas debo:
position.x = position.x + velocity.x;position.y = position.y + velocity.yDe esta manera, estás sumando las componentes x y y de los vectores de forma correcta. En el código, se está sumando x y xspeed, y y y yspeed, lo cual funciona bien para este caso, pero cuando trabajamos con objetos como vectores, necesitamos referenciar cada componente por separado.
Actividad 02
Repasa
Enunciado: realiza este ejercicio del libro Exercise 1.1
- ¿Que tuviste que hacer para hacer la conversión propuesta?
Entrega: el código del ejercicio.
🚀 Tu solución:
Ejemplo 0.1: Paseo aleatorio tradicional
¿Que tuviste que hacer para hacer la conversión propuesta?
- En lugar de tener las variables this.x y this.y como números independientes, use un p5.Vector que almacene ambas coordenadas.
- Modificación de step(): Cuando el caminante elige una dirección, vamos a sumarle un vector de desplazamiento. Por ejemplo, si el caminante se mueve a la derecha, agregamos un vector (1, 0).
- Actualización de la posición: En lugar de modificar this.x y this.y por separado, actualicé el vector de posición sumando un nuevo vector de acuerdo a la dirección elegida.
let walker;
function setup() { createCanvas(640, 240); walker = new Walker(); background(255);}
function draw() { walker.step(); walker.show();}
class Walker { constructor() { // Inicialice el vector de posición en el centro del lienzo this.position = createVector(width / 2, height / 2); }
show() { stroke(0); point(this.position.x, this.position.y); // Dibuje el punto usando el vector }
step() { // Elegimos una dirección aleatoria const choice = floor(random(4));
let step = createVector(0, 0); // Cree un vector de paso vacío
if (choice == 0) { step.x = 1; // Movimiento a la derecha } else if (choice == 1) { step.x = -1; // Movimiento a la izquierda } else if (choice == 2) { step.y = 1; // Movimiento hacia abajo } else { step.y = -1; // Movimiento hacia arriba }
// Sume el vector de paso a la posición actual this.position.add(step); }}Investigación
¡Es hora de explorar! En esta fase, profundizarás en la teoría y práctica de los vectores a través de la lectura del capítulo 1 del libro “The Nature of Code”. Realizarás experimentos, analizarás ejemplos y te familiarizarás con las diferentes funciones de p5.js para manipular vectores.
Actividad 03
Experimenta
Enunciado: dale una mirada a este código
let position;
function setup() { createCanvas(400, 400); posicion = createVector(6,9); playingVector(posicion); noLoop();}
function playingVector(v){ v.x = 20; v.y = 30;}
function draw() { background(220); console.log("Only once");}Para este experimento puedes usar las funciones console.log() y print() para imprimir mensajes en la consola del navegador. También puedes usar el método toString() de la clase p5.Vector para imprimir el vector en la consola.
- ¿Qué resultado esperas obtener?
- ¿Qué resultado obtuviste?
- Recuerda los conceptos de paso por valor y paso por referencia en programación. Muestra ejemplos de este concepto en javascript.
- ¿Qué tipo de paso se está realizando en el código?
- ¿Qué aprendiste?
Entrega: la solución a las preguntas.
🚀 Tu solución:
- funciones console.log() y print() para imprimir mensajes en la consola del navegador.
- método toString() de la clase p5.Vector para imprimir el vector en la consola.
Código
let position;
function setup() { createCanvas(400, 400); // Crea un lienzo de 400x400 píxeles posicion = createVector(6, 9); // Inicializa el vector con las coordenadas (6, 9) playingVector(posicion); // Modifica las componentes del vector noLoop(); // Detiene el loop de draw(), solo se ejecuta una vez}
function playingVector(v) { v.x = 20; // Modifica la componente x del vector a 20 v.y = 30; // Modifica la componente y del vector a 30}
function draw() { background(220); // Establece un fondo gris console.log("Only once"); // Imprime "Only once" en la consola, solo se ve una vez}¿Qué resultado esperas obtener?
No lo se, según lo que se dice con las funciones console.log() y print(), si utilizamos esto me imagino que deberá imprimir mensajes en la consola del navegador, que sería Only once.
¿Qué resultado obtuviste?
- Obtuve en la consola un Only once
- Un lienzo gris de 400 x 400
Recuerda los conceptos de paso por valor y paso por referencia en programación. Muestra ejemplos de este concepto en javascript.
Paso por valor: Ocurre cuando se pasan tipos de datos primitivos (números, cadenas, booleanos, etc.). Se crea una copia del valor original y cualquier cambio dentro de la función no afecta la variable original.
let a = 10;let b = a; // Se copia el valor de a en bb = 20; // Modificar b NO afecta a a
console.log(a); // 10console.log(b); // 20Paso por referencia: Ocurre cuando pasamos objetos, arreglos o vectores (p5.Vector). En este caso, se pasa una referencia, lo que significa que cualquier modificación dentro de una función afectará el objeto original.
let vectorA = createVector(5, 10);let vectorB = vectorA; // Ambos apuntan al mismo objetovectorB.x = 20; // Modifica el objeto original
console.log(vectorA.toString()); // "p5.Vector { x: 20, y: 10, z: 0 }"console.log(vectorB.toString()); // "p5.Vector { x: 20, y: 10, z: 0 }"¿Qué tipo de paso se está realizando en el código?
El paso que se realizo en el codigo fue paso por referencia. Esto es porque los objetos como los vectores en JavaScript se pasan por referencia, no por valor. Cuando pasas posicion a la función playingVector(), la función modifica directamente las propiedades x y y del vector original, no una copia de él.
let posicion = createVector(6, 9);playingVector(posicion);¿Qué aprendiste?
- El paso de objetos (como p5.Vector) en JavaScript se hace por referencia, lo que significa que cualquier cambio dentro de una función o modificación directa de ese objeto afecta a la variable original.
- El uso de toString() en un objeto p5.Vector nos permite ver su contenido en formato de texto y verificar cómo se comportan las modificaciones.
- noLoop(); en setup() detiene la ejecución continua de draw(), haciendo que los comandos dentro de draw() se ejecuten solo una vez.
- console.log() y print() nos ayudan a depurar el código imprimiendo valores en la consola del navegador.
Actividad 04
Explora posibilidades
Enunciado: dale una mirada a la clase p5.Vector aquí.
- ¿Para qué sirve el método mag()? Nota que hay otro método llamado magSq(). ¿Cuál es la diferencia entre ambos? ¿Cuál es más eficiente?
- ¿Para qué sirve el método normalize()?
- Te encuentras con un periodista en la calle y te pregunta ¿Para qué sirve el método dot()? ¿Qué le responderías en un frase?
- El método dot() tiene una versión estática y una de instancia. ¿Cuál es la diferencia entre ambas?
- Ahora el mismo periodista curioso de antes te pregunta si le puedes dar una intuición geométrica acerca del producto cruz. Entonces te pregunta ¿Cuál es la interpretación geométrica del producto cruz de dos vectores? Tu respuesta debe incluir qué pasa con la orientación y la magnitud del vector resultante.
- ¿Para que te puede servir el método dist()?
- ¿Para qué sirven los métodos normalize() y limit()?
Entrega: la solución a las preguntas
🚀 Tu solución:
¿Para qué sirve el método mag()? Nota que hay otro método llamado magSq(). ¿Cuál es la diferencia entre ambos? ¿Cuál es más eficiente?
Mag
- Calcula la magnitud (longitud) del vector.
- Utilice mag() para calcular la magnitud de un vector 2D utilizando componentes como en .mag(x, y)
Formula:
![]()
- Esto nos dice qué tan “largo” es el vector en el espacio.
magSq
-
Calcula la magnitud (longitud) del vector al cuadrado.
Formula:
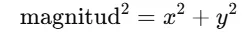
-
.magSq() calcula la magnitud al cuadrado, sin aplicar la raíz cuadrada.
-
La diferencia es que magSq() no usa la raíz cuadrada, lo que lo hace más eficiente.
-
magSq() es más rápido que mag() porque evita la operación de raíz cuadrada (sqrt()), que es costosa en términos de rendimiento.
-
Si solo necesito comparar magnitudes de vectores (por ejemplo, saber cuál es más largo), es mejor usar magSq() en lugar de mag(), ya que es más eficiente.
¿Para qué sirve el método normalize()?
-
Escala los componentes de un p5. Objeto vectorial de modo que su magnitud sea 1.
-
La versión estática de , como en , devuelve un nuevo p5. Vector y no cambia el original.normalize()p5.Vector.normalize(v).
-
Para normalizar un vector, se divide cada componente entre su magnitud:
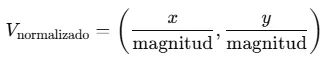
Te encuentras con un periodista en la calle y te pregunta ¿Para qué sirve el método dot()? ¿Qué le responderías en un frase?
-Calcula el producto escalar entre dos vectores.
- El producto escalar es un número que indica cuánto se parecen en dirección.
- Si los vectores son paralelos, el resultado es grande.
- Si son perpendiculares (90°), el resultado es 0.
- Si apuntan en direcciones opuestas, el resultado es negativo.
- La versión con un parámetro lo interpreta como otro p5. Objeto vectorial.dot()
- La versión con varios parámetros los interpreta como los componentes , , y de otro vector.dot()xyz
- La versión estática de , como en , es lo mismo que llamar a .dot()p5.Vector.dot(v1, v2)v1.dot(v2)o
Le diría que “El método dot() calcula el producto escalar de dos vectores. Es como medir cuánto se parecen en dirección. Si son paralelos, el resultado es grande; si son perpendiculares, es 0.”
El método dot() tiene una versión estática y una de instancia. ¿Cuál es la diferencia entre ambas?
La diferencia entre la versión estática y la versión de instancia del método dot() en p5.js es la forma en que se usa:
Versión de instancia (v1.dot(v2))
- Se usa en un objeto vector existente.
- Se llama desde el propio vector y recibe otro vector o coordenadas como argumento.
Versión estática (p5.Vector.dot(v1, v2)):
-
Se usa sin necesidad de tener un vector creado antes.
-
Se llama directamente desde la clase p5.Vector y recibe dos vectores como argumentos.
-
Usar v1.dot(v2) si ya tengo un vector y quieres compararlo con otro.
-
Usar p5.Vector.dot(v1, v2) si necesito calcular el producto escalar sin modificar un vector específico.
Ahora el mismo periodista curioso de antes te pregunta si le puedes dar una intuición geométrica acerca del producto cruz. Entonces te pregunta ¿Cuál es la interpretación geométrica del producto cruz de dos vectores? Tu respuesta debe incluir qué pasa con la orientación y la magnitud del vector resultante.
- Calcula el producto cruzado de dos vectores.
- El producto cruzado es un vector que apunta directamente fuera del plano creado por dos vectores. La magnitud del producto cruzado es el área del paralelogramo formado por los dos vectores originales.
- La versión estática de , como en , es lo mismo que llamar a .cross()p5.Vector.cross(v1, v2)v1.cross(v2)
El producto cruz de dos vectores tiene una interpretación geométrica clara:
1. El resultado es un nuevo vector perpendicular
Si trabajas en 3D, el producto cruz de dos vectores genera un tercer vector perpendicular a ambos. Es como si los vectores iniciales formaran un “plano”, y el vector resultante apunta fuera de ese plano.
2. La magnitud representa el área del paralelogramo
La longitud del vector resultante es igual al área del paralelogramo formado por los dos vectores originales. Si los vectores son paralelos, el área es cero y el producto cruz también.
3. La orientación sigue la regla de la mano derecha
Si apuntas tu mano derecha con los dedos en la dirección del primer vector y los cierras hacia el segundo vector, el pulgar apunta en la dirección del vector resultante.
¿Para que te puede servir el método dist()?
El método dist() sirve para calcular la distancia entre dos puntos en el espacio.
- Mide qué tan lejos están dos puntos: Si tengo dos puntos en un plano o en el espacio, dist() te dice la distancia entre ellos.
- Las coordenadas de un punto se pueden representar mediante los componentes de un vector que se extiende desde el origen hasta el punto.
- La versión estática de , como en , es lo mismo que llamar a .dist()p5.Vector.dist(v1, v2)v1.dist(v2)
Utilice dist() para calcular la distancia entre puntos utilizando coordenadas como en .dist(x1, y1, x2, y2)
¿Para qué sirven los métodos normalize() y limit()?
Normalize
- Sirve para convertir un vector en una versión más pequeña pero con la misma dirección.
- Básicamente, “estira” o “encoge” el vector para que su tamaño sea exactamente 1.
- Se usa cuando solo importa la dirección del vector, no su tamaño.
Ejemplo:
Si un vector es (3,4), al normalizarlo se convertirá en (~0.6, ~0.8), pero seguirá apuntando en la misma dirección
let v = createVector(3, 4);v.normalize();console.log(v); // Ahora su magnitud es 1Límit
- Si un vector es demasiado grande, limit() lo reduce a un máximo permitido, limita la magnitud de un vector a un valor máximo.
- Funciona como un “freno” para que no crezca más allá de cierto tamaño.
- La versión estática de , como en , devuelve un nuevo p5. Vector y no cambia el original.limit()p5.Vector.limit(v, 5)
Ejemplo:
Si un vector tiene magnitud 10 y usamos limit(5), su tamaño bajará a 5, pero mantendrá la dirección.
let v = createVector(10, 10);v.limit(5);console.log(v); // Su magnitud no será mayor a 5Actividad 05
Interpolamos?
Enunciado: vas a tomar como inspiración este ejemplo de la referencia de p5.js:
function setup() { createCanvas(100, 100);}
function draw() { background(200);
let v0 = createVector(50, 50); let v1 = createVector(30, 0); let v2 = createVector(0, 30); let v3 = p5.Vector.lerp(v1, v2, 0.5); drawArrow(v0, v1, 'red'); drawArrow(v0, v2, 'blue'); drawArrow(v0, v3, 'purple');}
function drawArrow(base, vec, myColor) { push(); stroke(myColor); strokeWeight(3); fill(myColor); translate(base.x, base.y); line(0, 0, vec.x, vec.y); rotate(vec.heading()); let arrowSize = 7; translate(vec.mag() - arrowSize, 0); triangle(0, arrowSize / 2, 0, -arrowSize / 2, arrowSize, 0); pop();}Vas a modificarlo para generar este resultado:
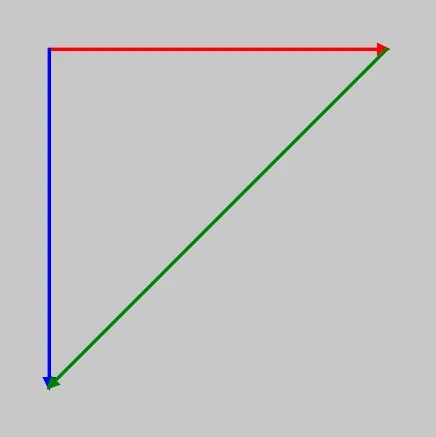
- Analiza cómo funciona el método lerp().
- Nota que además de la interpolación lineal de vectores, también puedes hacer interpolación lineal de colores con el método lerpColor().
Dedica un tiempo a estudiar cómo se dibuja una flecha en el método drawArrow().
Entrega:
- El código que genera el resultado propuesto.
- ¿Cómo funciona lerp() y lerpColor().
- ¿Cómo se dibuja una flecha usando drawArrow()?
🚀 Tu solución:
Codigo de analisis:
function setup() { createCanvas(100, 100);}
function draw() { background(200);
//Creación vectores let v0 = createVector(50, 50); // Origen de los vectores (punto de inicio) let v1 = createVector(30, 0); // Vector rojo (horizontal) let v2 = createVector(0, 30); // Vector azul (vertical)
//Interpolación Lineal con lerp() let v3 = p5.Vector.lerp(v1, v2, 0.5); // Crea v3, un vector intermedio entre v1 y v2 // Toma un punto a mitad de camino entre v1 y v2.
//Dibuja los vectores drawArrow(v0, v1, 'red'); drawArrow(v0, v2, 'blue'); drawArrow(v0, v3, 'purple');}
function drawArrow(base, vec, myColor) { push(); stroke(myColor); // Color de la flecha strokeWeight(3); // Grosor de la línea fill(myColor);
translate(base.x, base.y); // Mueve el origen de coordenadas a `base`
line(0, 0, vec.x, vec.y); // Dibuja la línea desde (0,0) hasta (vec.x, vec.y)
rotate(vec.heading()); // Rota en la dirección del vector
let arrowSize = 7; translate(vec.mag() - arrowSize, 0); // Mueve el punto de la flecha
triangle(0, arrowSize / 2, 0, -arrowSize / 2, arrowSize, 0); // Dibuja la punta de la flecha
pop();}El código que genera el resultado propuesto.
- Agrande el canvas a 400x400
- Alargue los vectores
- Calculé un vector verde: Utilicé p5.Vector.sub(v2, v1) para calcular la diferencia entre los vectores v1 y v2, lo que da el vector verde que conecta estos dos puntos.
- Usé p5.Vector.add(v0, v1) para mover el punto de origen de la flecha verde correctamente, de modo que esta se conecte a las otras flechas.
- Dibujo la flecha
- Añadí suavizado de movimiento: En lugar de incrementar t con un valor constante (t += 0.01),use lerp() para que fuera mas fluida y controlada para suavizar el movimiento.
- Rebote de la animación: Implementamos un rebote de la flecha morada utilizando la variable t para controlar su interpolación, y cambiamos la dirección de la animación cuando alcanza los valores 0 o 1. -Interapolarmos colores con Lerpcolor:
let t = 0; // Controlador de la interpolaciónlet direction = 1; // Dirección de la animación (1 = avanzando, -1 = retrocediendo)
function setup() { createCanvas(400, 400);}
function draw() { background(200);
let v0 = createVector(30, 50); let v1 = createVector(300, 0); let v2 = createVector(0, 300);
// Calcula la interpolación entre v1 y v2 con t variando de 0 a 0.99 let v3 = p5.Vector.lerp(v1, v2, t);
// Calcula los vectores entre v1 y v2 (verde) let vGreen = p5.Vector.sub(v2, v1);
// Colores a interpolar let redColor = color(255, 0, 0); // Rojo let purpleColor = color(128, 0, 128); // Morado let blueColor = color(0, 0, 255); // Azul
// Interpolación de colores let currentColor; if (t < 0.5) { // De rojo a morado currentColor = lerpColor(redColor, purpleColor, t * 2); // Multiplicamos por 2 para que el cambio ocurra más rápido en la primera mitad } else { // De morado a azul currentColor = lerpColor(purpleColor, blueColor, (t - 0.5) * 2); // Multiplicamos por 2 para que el cambio ocurra más rápido en la segunda mitad }
// Dibuja las flechas drawArrow(v0, v1, 'red'); // Flecha roja de v0 a v1 drawArrow(v0, v2, 'blue'); // Flecha azul de v0 a v2 drawArrow(v0, v3, currentColor); // Flecha morada con color interpolado drawArrow(p5.Vector.add(v0, v1), vGreen, 'green'); // Flecha verde de v1 a v2
// Actualiza t, el valor de interpolación, para mover la flecha t += 0.01 * direction;
// Cambia la dirección cuando t llegue a 0 o 1 if (t >= 1 || t <= 0) { direction *= -1; }}
function drawArrow(base, vec, myColor) { push(); stroke(myColor); strokeWeight(3); fill(myColor); translate(base.x, base.y); line(0, 0, vec.x, vec.y); rotate(vec.heading()); let arrowSize = 7; translate(vec.mag() - arrowSize, 0); triangle(0, arrowSize / 2, 0, -arrowSize / 2, arrowSize, 0); pop();}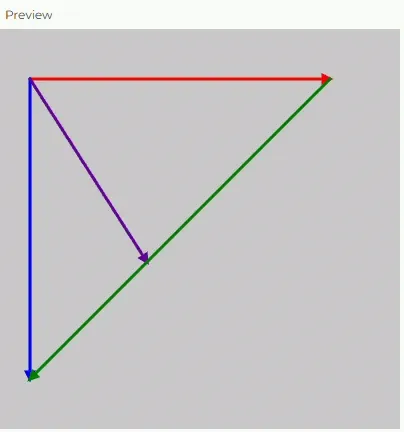
¿Cómo funciona lerp() y lerpColor().
lerp()
- Es una función de interpolación lineal que se utiliza para calcular un valor intermedio entre dos números. Se expresa como lerp(start, stop, amt), donde:
- start: El valor de inicio (el valor desde el cual se empieza).
- stop: El valor final (el valor al cual se quiere llegar).
- amt: Un número entre 0 y 1 que representa la cantidad de interpolación entre el valor de inicio y el valor final. Si amt = 0, el valor es igual a start; si amt = 1, el valor es igual a stop; valores intermedios producen valores interpolados.
En el contexto de los vectores, como hicimos en el código, lerp() calcula un punto intermedio entre dos vectores. P5.Vector.lerp(v1, v2, t) nos da un vector en la línea que conecta v1 y v2, dependiendo de la proporción de t. Cuando t varía entre 0 y 1, el vector se mueve gradualmente de v1 a v2.
lerpColor():
lerpColor() es similar a lerp(), pero en lugar de trabajar con números, trabaja con colores. La función se usa de la forma lerpColor(color1, color2, amt), donde:
- color1: El primer color de inicio.
- color2: El color final al que quieres llegar.
- amt: La cantidad de interpolación, que también varía entre 0 y 1. Cuando amt = 0, el color será igual a color1, y cuando amt = 1, el color será igual a color2. Los valores intermedios crean un gradiente suave entre los dos colores.
En el código, usé lerpColor() para cambiar el color de la flecha morada, pasando de rojo a morado y luego de morado a azul, dependiendo del valor de t.
¿Cómo se dibuja una flecha usando drawArrow()?
drawArrow():
Es una función personalizada que dibuja una flecha en el lienzo. Se usa de la siguiente forma: drawArrow(base, vec, myColor), donde:
- base: El punto de inicio de la flecha (un vector). Es el punto desde donde la flecha comienza a dibujarse.
- vec: El vector que define la dirección y magnitud de la flecha. Este vector determina hacia dónde apunta la flecha y cuánto mide.
- myColor: El color de la flecha. Se pasa como un valor de color (por ejemplo, color(255, 0, 0) para rojo).
- push() y pop(): Se usan para guardar y restaurar el estado de las transformaciones, como la posición y rotación, para que no afecten a otros dibujos.
- translate(base.x, base.y): Desplaza el origen del sistema de coordenadas a las coordenadas del vector base.
- line(0, 0, vec.x, vec.y): Dibuja una línea desde el origen (0, 0) hasta las coordenadas del vector vec que define la dirección y magnitud de la flecha.
- rotate(vec.heading()): Rota el sistema de coordenadas para que la línea se dibuje en la dirección correcta.
- triangle(0, arrowSize / 2, 0, -arrowSize / 2, arrowSize, 0): Dibuja el triángulo de la punta de la flecha, ubicado en la dirección final del vector, para representar la punta de la flecha.
Esto permite crear flechas que se dibujan con el color y la orientación que definimos, adaptándose a las coordenadas de los vectores que se pasan como argumentos.
Actividad 06
Hagamos que todo se mueva
Enunciado: modifica de nuevo el programa de la actividad anterior, pero esta vez cambia la base de las flechas y la escala de los vectores usando el mouse.
Entrega:
- Código con la modificación.
- Explica cómo solucionaste el problema.
🚀 Tu solución:
modifica de nuevo el programa de la actividad anterior, pero esta vez cambia la base de las flechas y la escala de los vectores usando el mouse.
Código con la modificación.
let t = 0; // Controlador de la interpolaciónlet direction = 1; // Dirección de la animación (1 = avanzando, -1 = retrocediendo)
function setup() { createCanvas(400, 400);}
function draw() { background(200);
// Base completamente dentro del canvas let baseX = constrain(mouseX, 0, width); let baseY = constrain(mouseY, 0, height); let base = createVector(baseX, baseY);
// Factor de escala basado en la posición del mouse let scaleFactor = constrain(map(mouseX, 0, width, 0.5, 1.5), 0.5, 1.5);
// Vectores escalados let v1 = createVector(200, 0).mult(scaleFactor); let v2 = createVector(0, 200).mult(scaleFactor);
// Asegurar que los vectores no salgan del canvas v1.limit(width - baseX); v2.limit(height - baseY);
// Vector interpolado entre v1 y v2 let v3 = p5.Vector.lerp(v1, v2, t);
// Vector verde entre v1 y v2 let vGreen = p5.Vector.sub(v2, v1);
// Colores a interpolar let redColor = color(255, 0, 0); let purpleColor = color(128, 0, 128); let blueColor = color(0, 0, 255);
// Interpolación de colores let currentColor; if (t < 0.5) { currentColor = lerpColor(redColor, purpleColor, t * 2); } else { currentColor = lerpColor(purpleColor, blueColor, (t - 0.5) * 2); }
// Dibujar flechas drawArrow(base, v1, 'red'); drawArrow(base, v2, 'blue'); drawArrow(base, v3, currentColor); drawArrow(p5.Vector.add(base, v1), vGreen, 'green');
// Actualizar t para la animación t += 0.01 * direction;
// Cambiar la dirección cuando t llegue a 0 o 1 if (t >= 1 || t <= 0) { direction *= -1; }}
function drawArrow(base, vec, myColor) { push(); stroke(myColor); strokeWeight(3); fill(myColor); translate(base.x, base.y); line(0, 0, vec.x, vec.y); rotate(vec.heading()); let arrowSize = 7; translate(vec.mag() - arrowSize, 0); triangle(0, arrowSize / 2, 0, -arrowSize / 2, arrowSize, 0); pop();}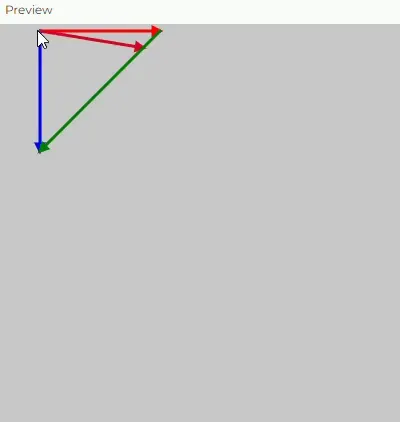
Explica cómo solucionaste el problema
1. Cambio de la base de las flechas usando el mouse
- Antes, la base de las flechas estaba en una posición fija (v0 = createVector(30, 50)), pero tenía que moverse según el mouse.
- Se usa mouseX y mouseY para definir la nueva base
let baseX = constrain(mouseX, 0, width);let baseY = constrain(mouseY, 0, height);let base = createVector(baseX, baseY);2. Escalado de los vectores con el mouse
- Creé un factor de escala basado en mouseX, para hacer que los vectores cambien de tamaño dinámicamente
let scaleFactor = constrain(map(mouseX, 0, width, 0.5, 1.5), 0.5, 1.5);- map() toma el valor de mouseX y lo convierte en un rango de 0.5 a 1.5 para evitar que los vectores sean demasiado pequeños o grandes.
3. Límites para que los vectores no se salieran del canvas
- Utilicé .limit() a los vectores v1 y v2 para asegurarme de que no crecieran más allá del borde de canvas:
v1.limit(width - baseX);v2.limit(height - baseY);Actividad 07
Motion 101
Entrega: ahora vas a leer y analizar con mucho detenimiento la sección Motion with vectors. El autor propone un marco de movimiento llamado motion 101.
¿En qué consiste motion 101?
Entrega: la respuesta a la pregunta e ilustra con un ejemplo.
🚀 Tu solución:
¿En qué consiste motion 101?
Motion 101
- Suma la velocidad a la posición → Esto hace que el objeto se mueva.
- Dibuja el objeto en la posición → Para que el movimiento sea visible en el lienzo.
En Motion 101, cada objeto en movimiento tiene dos propiedades clave:
- Posición (position) → Define dónde está el objeto.
- Velocidad (velocity) → Define qué tan rápido y en qué dirección se mueve.
Cada cuadro (draw() en p5.js), el programa actualiza la posición sumando la velocidad. Si no se modifica la velocidad, el objeto se moverá en línea recta constantemente.
Encapsulación en una Clase (Mover)
Para organizar mejor el código y hacer objetos reutilizables, se encapsula este comportamiento en una clase. Una clase Mover puede incluir:
-
Datos:
- position (posición del objeto)
- velocity (velocidad del objeto)
-
Funcionalidad:
- update() → Actualiza la posición sumando la velocidad.
- display() → Dibuja el objeto en su nueva posición.
- checkEdges() → Detecta colisiones con los bordes para hacer que rebote.
Así, el objeto se mueve por sí solo sin tener que escribir todo el código dentro de draw().
Ejemplo:
//La clase Mover encapsula el comportamiento del objeto en movimientoclass Mover { constructor() { this.position = createVector(random(width), random(height)); // Posición inicial aleatoria this.velocity = createVector(random(-4, 5), random(-4, 5)); // Velocidad aleatoria }// Aplicación Motion 101, haciendo que el objeto se mueva update() { this.position.add(this.velocity); // Motion 101: Sumar velocidad a la posición }//Verifica si el objeto se ha salido del lienzo y lo hace rebotar si es necesario checkEdges() { if (this.position.x > width || this.position.x < 0) { this.velocity.x *= -1; // Rebote horizontal } if (this.position.y > height || this.position.y < 0) { this.velocity.y *= -1; // Rebote vertical } }
display() { fill(255, 0, 0); ellipse(this.position.x, this.position.y, 20, 20); }}
let mover;//Variable global mover para almacenar la instancia de la clase
function setup() { createCanvas(400, 400); mover = new Mover(); //Crea un nuevo objeto Mover, inicializándolo con una posición y velocidad aleatorias.}
function draw() { background(220); mover.update(); //Actualiza la posición del objeto mover.checkEdges(); // Verifica si se ha salido del lienzo y lo hace rebotar mover.display();// Dibuja el objeto en la nueva posición}
Actividad 08
Experimenta
Enunciado: realiza un experimento para basado en el ejemplo 1.7.
- Entiende el ejemplo.
- Vas a proponer una modificación mediante esta pregunta que te harás: ¿Qué pasa si…?
- ¿Qué te imaginas que pasará?
- ¿Qué pasó?
- ¿Por qué?
- Concluye
Entrega: la respuesta a las cuestiones anteriores.
🚀 Tu solución:
Entendimiento del ejemplo.
- Crea un objeto Mover que se mueve solo.
- Cuando toca los bordes, aparece en el lado opuesto (como un juego de Pac-Man).
- Se actualiza y se redibuja en cada frame.
// Declaramos la variable global para el objeto Mover.let mover;
function setup() { createCanvas(640, 240); // Creamos un lienzo de 640x240 píxeles. mover = new Mover(); // Inicializamos el objeto Mover.}
function draw() { background(255); // Limpiamos la pantalla con un fondo blanco en cada frame.
mover.update(); // Actualizamos la posición del objeto. mover.checkEdges(); // Verificamos si el objeto toca los bordes. mover.show(); // Dibujamos el objeto en su nueva posición.}
class Mover { constructor() { // La posición inicial será un punto aleatorio dentro del canvas. this.position = createVector(random(width), random(height));
// La velocidad inicial será un vector con valores aleatorios entre -2 y 2 en x e y. this.velocity = createVector(random(-2, 2), random(-2, 2)); }
update() { // La posición cambia sumando la velocidad en cada frame. this.position.add(this.velocity); }
show() { stroke(0); // Borde negro. strokeWeight(2); // Grosor del borde. fill(127); // Relleno gris. circle(this.position.x, this.position.y, 48); // Dibujamos el círculo en su posición actual. }
checkEdges() { // Si la posición X supera el ancho del lienzo, reaparece en X = 0. if (this.position.x > width) { this.position.x = 0; } // Si la posición X es menor a 0, reaparece en X = ancho del lienzo. else if (this.position.x < 0) { this.position.x = width; }
// Si la posición Y supera la altura del lienzo, reaparece en Y = 0. if (this.position.y > height) { this.position.y = 0; } // Si la posición Y es menor a 0, reaparece en Y = altura del lienzo. else if (this.position.y < 0) { this.position.y = height; } }}Vas a proponer una modificación mediante esta pregunta que te harás: ¿Qué pasa si…?
¿Qué pasa si las bolas cambian de color al cruzar los bordes y dejan un rastro de su movimiento?
¿Qué te imaginas que pasará?
Espero que las bolas se muevan aleatoriamente y, cada vez que salgan del canvas, reaparezcan del otro lado con un color diferente. Como el fondo no se borra, deberían dejar un rastro de colores en la pantalla, y va a ser una combinación de muchos colores
¿Qué pasó?
Las bolas efectivamente cambian de color cada vez que cruzan los bordes. También se va formando un patrón visual de líneas de colores debido a que no se borra el fondo en draw()
¿Por qué?
Cuando una bola llega al borde del canvas, se reposiciona del otro lado, y en ese momento cambia su color. Como el fondo no se reinicia, su trayectoria se va dibujando en la pantalla.
Conclusión
Este experimento muestra cómo se puede generar un efecto visual interesante simplemente modificando la forma en que se actualiza la posición y el color de los objetos. Además, demuestra cómo la persistencia del rastro crea un efecto artístico llamativo.
Codigo
let movers = [];let numMovers = 5; // Cantidad inicial de bolas
function setup() { createCanvas(640, 480); for (let i = 0; i < numMovers; i++) { movers.push(new Mover()); }}
function draw() { // No usamos background para dejar el rastro de movimiento. for (let mover of movers) { mover.update(); mover.checkEdges(); mover.show(); }}
class Mover { constructor() { // Posición y velocidad aleatoria. this.position = createVector(random(width), random(height)); this.velocity = createVector(random(-7, 5), random(-7, 5)); this.color = color(random(255), random(255), random(255)); // Color inicial aleatorio. }
update() { this.position.add(this.velocity); }
checkEdges() { let rebote = false;
if (this.position.x > width) { this.position.x = 0; rebote = true; } else if (this.position.x < 0) { this.position.x = width; rebote = true; }
if (this.position.y > height) { this.position.y = 0; rebote = true; } else if (this.position.y < 0) { this.position.y = height; rebote = true; }
// Si la bola sale del canvas, cambia de color. if (rebote) { this.color = color(random(255), random(255), random(255)); } }
show() { fill(this.color); noStroke(); circle(this.position.x, this.position.y, 20); }}
Actividad 09
Experimentando con la aceleración
Enunciado: en el libro proponen una regla (que eventualmente se rompe cuando conviene :)):
The goal for programming motion is to come up with an algorithm for calculating acceleration and then let the trickle-down effect work its magic.
Para investigador el significado de esta frase te propone que construyas un experimento donde analices cómo se comporta un objeto en movimiento con:
- Aceleración constante.
- Aceleración aleatoria.
- Aceleración hacia el mouse.
Entrega:
- Reporta que encontraste para cada una de las posibles aceleraciones
- ¿Por qué?
🚀 Tu solución:
Experimento
Aceleración constante.
let mover;
function setup() { createCanvas(640, 480); mover = new Mover();}
function draw() { background(255); mover.update(); mover.checkEdges(); mover.show();}
class Mover { constructor() { this.position = createVector(width / 2, height / 2); // Posición inicial en el centro this.velocity = createVector(0, 0); // Velocidad inicial en 0 this.acceleration = createVector(0.1, 0.1); // Aceleración constante en x y y }
update() { this.velocity.add(this.acceleration); // Aumenta la velocidad con la aceleración this.position.add(this.velocity); // Mueve la posición con la velocidad }
checkEdges() { if (this.position.x > width || this.position.x < 0) { this.velocity.x *= -1; // Rebote en los bordes horizontales } if (this.position.y > height || this.position.y < 0) { this.velocity.y *= -1; // Rebote en los bordes verticales } }
show() { fill(0); noStroke(); circle(this.position.x, this.position.y, 20); // Dibuja la bola }}La aceleración constante hace que la velocidad se incremente progresivamente, lo que provoca un movimiento cada vez más rápido. Al chocar con los bordes, la dirección de la velocidad se invierte.
Aceleración aleatoria.
let mover;
function setup() { createCanvas(640, 480); mover = new Mover();}
function draw() { background(255); mover.update(); mover.checkEdges(); mover.show();}
class Mover { constructor() { this.position = createVector(width / 2, height / 2); // Comienza en el centro this.velocity = createVector(0, 0); // Velocidad inicial en 0 }
update() { let acceleration = createVector(random(-1, 1), random(-1, 1)); // Aceleración con cambios más bruscos this.velocity.add(acceleration); // La velocidad cambia con cada frame this.velocity.limit(8); // Limitamos la velocidad máxima this.position.add(this.velocity); // Se mueve según la velocidad }
checkEdges() { if (this.position.x > width || this.position.x < 0) { this.velocity.x *= -1; // Rebote en los bordes } if (this.position.y > height || this.position.y < 0) { this.velocity.y *= -1; } }
show() { fill(0); noStroke(); circle(this.position.x, this.position.y, 20); }}La aceleración aleatoria cambia en cada frame, lo que hace que la dirección del movimiento sea impredecible. Esto imita el comportamiento de partículas en un fluido o incluso el movimiento de algunas bacterias.
- Cada frame, la aceleración cambia aleatoriamente en un pequeño rango.
- La velocidad se ajusta con la aceleración, causando que la bola se mueva de forma errática.
- El objeto rebota en los bordes, invirtiendo su dirección. Aceleración hacia el mouse.
let mover;
function setup() { createCanvas(640, 480); mover = new Mover();}
function draw() { background(255); mover.update(); mover.checkEdges(); mover.show();}
class Mover { constructor() { this.position = createVector(width / 2, height / 2); // Comienza en el centro this.velocity = createVector(0, 0); // Velocidad inicial en 0 }
update() { let mouse = createVector(mouseX, mouseY); // Posición del mouse let acceleration = p5.Vector.sub(mouse, this.position); // Calcula el vector hacia el mouse acceleration.setMag(0.1); // Define la magnitud de la aceleración
this.velocity.add(acceleration); // Agrega aceleración a la velocidad this.velocity.limit(5); // Limita la velocidad máxima this.position.add(this.velocity); // Mueve la posición }
checkEdges() { if (this.position.x > width || this.position.x < 0) { this.velocity.x *= -1; // Rebote en los bordes } if (this.position.y > height || this.position.y < 0) { this.velocity.y *= -1; } }
show() { fill(0); noStroke(); circle(this.position.x, this.position.y, 20); }}- Se calcula un vector desde la bola hasta el mouse con p5.Vector.sub(mouse, this.position).
- La aceleración se establece con setMag(0.1), lo que significa que siempre será una fuerza constante, pero en la dirección del mouse.
- La velocidad aumenta en la dirección del mouse y se limita a 5 para evitar que sea demasiado rápida.
- Si la bola choca con los bordes, se rebota.
Explicación frase
The goal for programming motion is to come up with an algorithm for calculating acceleration and then let the trickle-down effect work its magic. La frase dice que el objetivo al programar el movimiento es encontrar un algoritmo para calcular la aceleración, y luego dejar que el “trickle-down effect” haga su magia.
¿Qué significa esto en nuestros experimentos?
- Primero definimos cómo cambia la aceleración (constante, aleatoria o dirigida al mouse).
- Luego, esa aceleración afecta la velocidad (hace que aumente o cambie).
- Finalmente, la velocidad modifica la posición del objeto.
Este es el “trickle-down effect” → La aceleración genera cambios en la velocidad y estos afectan el movimiento.
Los experimentos lo demostraron:
- Con aceleración constante → La bola se iba moviendo cada vez más rápido.
- Con aceleración aleatoria → La bola cambiaba de dirección de manera errática.
La clave en la animación de movimiento no es solo la velocidad, sino cómo se calcula y aplica la aceleración.
Aplicación
En esta fase, aplicarás tus conocimientos sobre vectores para crear arte generativo algorítmico. Pondrás en práctica los conceptos aprendidos en las fases anteriores.
Actividad 10
Diseño: exploración de la idea
Enunciado: diseña una aplicación interactiva en tiempo que utilice los conceptos que investigaste. La aplicación debe:
- Generar una pieza de arte generativo algorítmico.
- Debes aplicar el marco MOTION 101.
- El contenido generado debe ser interactivo. Puedes utilizar mouse, teclado, cámara, micrófono, etc, para variar los parámetros del algoritmo en tiempo real.
Entrega:
- Un texto donde expliques tu intención de diseño.
- ¿Cómo piensas aplicar el marco MOTION 101 y por qué estos?
- Reporta los referentes que usaste para inspirarte.
🚀 Tu solución:
Idea 🫐
Intención de Diseño
El objetivo de esta aplicación es crear una versión interactiva de La Noche Estrellada de Vincent van Gogh, utilizando un sistema de partículas que se comportan como pinceladas en movimiento. Las partículas reaccionarán a la interacción del usuario y se desplazarán siguiendo patrones similares a los remolinos de la pintura original.
¿Cómo piensas aplicar el marco MOTION 101 y por qué estos?
Aplicaré MOTION 101 modelando cada partícula con los tres componentes clave:
- Posición: Determina dónde está cada partícula en el lienzo.
- Velocidad: Define la dirección y rapidez con la que se mueve la partícula.
- Aceleración: En este caso, usaré aceleración hacia el mouse, lo que hará que las partículas se vean atraídas por el cursor, generando una sensación de movimiento fluido e interactivo.
Reporta los referentes que usaste para inspirarte.
- La Noche Estrellada de Vincent van Gogh (por sus colores y trazos dinámicos)
- Patrik Hübner
Cambio de idea: 👁️
Intención de Diseño
Mi intención con esta simulación es representar un iris en movimiento dinámico, evocando la sensación de un ojo vivo y cambiante. Utilizando partículas dispuestas en patrones concéntricos, el objetivo es crear un efecto hipnótico y envolvente, donde la aceleración y el color aporten fluidez y profundidad a la imagen.
¿Cómo piensas aplicar el marco MOTION 101 y por qué estos?
Aplicaré MOTION 101 modelando cada partícula con los tres componentes clave:
- Posición: Cada partícula sigue una trayectoria circular alrededor del centro del iris, manteniendo un patrón estructurado.
- Velocidad: Se asigna una velocidad angular individual para dar la sensación de movimiento independiente en cada partícula.
- Aceleración: Implementé una aceleración dependiente del movimiento del mouse. Si el usuario mueve el mouse a la derecha, el iris gira más rápido; si lo mueve a la izquierda, el giro se ralentiza. Esto introduce un control interactivo y dinámico en la simulación.
Además, aplico lerp() para suavizar los cambios en la distancia radial de las partículas, dando un efecto más orgánico, y lerpColor() para crear transiciones suaves en los colores del iris, reforzando la estética viva y natural.
Reporta los referentes que usaste para inspirarte.
- El iris humano y sus patrones: Observé imágenes macro de ojos humanos para entender cómo los patrones de pigmentación crean estructuras radiales.
- Van Gogh y el movimiento en el arte: La fluidez y el uso del color en Starry Night inspiraron la forma en que las partículas se mueven y cambian de color.
- Simulaciones de partículas interactivas: Exploré proyectos en p5.js y Processing donde las partículas responden a la entrada del usuario, lo que me llevó a implementar la aceleración según el movimiento del mouse.
- Patrik Hübner
Actividad 11
Materialización
Enunciado: vas a implementar tu aplicación diseñada.
Entrega:
- Código de la aplicación.
- Captura del contenido generado.
- En caso de realizar alguna variación al concepto original, escribe un texto donde expliques la razón del cambio.
🚀 Tu solución:
Enlace al proyecto
Código de la aplicación.
let particles = [];let numParticles = 6000;let center;let colors;let a = 0;let b = 0.4;let prevMouseX;
function setup() { createCanvas(600, 600); center = createVector(width / 2, height / 2); colors = [ color('#8B4513'), // SaddleBrown color('#A0522D'), // Sienna color('#CD853F'), // Peru color('#D2691E'), // Chocolate color('#F4A460'), // SandyBrown color('#DEB887'), // BurlyWood color('#D2B48C'), // Tan color('#DAA520'), // GoldenRod color('#C19A6B') // Light Brown ];
for (let i = 0; i < numParticles; i++) { particles.push(new Particle(random(TWO_PI), random(50, 250))); }
frameRate(60); prevMouseX = mouseX;}
function draw() { background(0); translate(width / 2, height / 2); rotate(radians(a));
for (let p of particles) { p.update(); p.show(); }
// Dibujar la pupila con efecto dinámico y aceleración constante for (let i = 0; i < 300; i++) { let angle = random(TWO_PI); let radius = random(10, 40); let x = radius * cos(angle); let y = radius * sin(angle); fill(255, random(100, 255)); noStroke(); ellipse(x, y, random(2, 6)); }
// Ajustar velocidad de rotación según movimiento del mouse con mayor efecto let mouseSpeed = mouseX - prevMouseX; if (mouseSpeed > 0) { b = map(mouseSpeed, 0, width, 0.1, 0.5); } else if (mouseSpeed < 0) { b = map(abs(mouseSpeed), 0, width, 0.05, 0.2); } prevMouseX = mouseX;
a += b;}
class Particle { constructor(angle, radius) { this.angle = angle; this.radius = radius; this.baseRadius = radius; this.speed = random(0.002, 0.008); this.colorA = colors[int(random(colors.length))]; this.colorB = colors[int(random(colors.length))]; this.lerpFactor = random(0.01, 0.05); this.color = this.colorA; }
update() { this.angle += this.speed; this.radius = lerp(this.radius, this.baseRadius + sin(frameCount * 0.01) * 10, 0.1); this.color = lerpColor(this.color, this.colorB, this.lerpFactor);
if (frameCount % 100 == 0) { this.colorA = this.colorB; this.colorB = colors[int(random(colors.length))]; } }
show() { let x = this.radius * cos(this.angle); let y = this.radius * sin(this.angle);
fill(this.color); noStroke(); ellipse(x, y, 5); }}Captura del contenido generado.
Consolidación y matacognión
En esta fase final, reflexionarás sobre tu proceso de aprendizaje. Analizarás tus logros, identificarás áreas de mejora y consolidarás tu comprensión de los vectores y su aplicación.
Actividad 12
Análisis de resultados
Enunciado: revisa los resultados de las actividades de la fase APPLY. ¿Qué desafíos encontraste al aplicar los conceptos aprendidos? ¿Qué aprendiste de estos desafíos?
Entrega: descripción de los desafíos encontrados y las lecciones aprendidas durante la fase APPLY.
🚀 Tu solución:
¿Qué desafíos encontraste al aplicar los conceptos aprendidos?
- Me toco cambiar la idea por que la primera era un poco mas complicada y no sabia como ejercutarla de una manera correcta.
- Uno de los principales desafíos fue mantener la coherencia visual del iris mientras aplicaba los conceptos de MOTION 101. Al agregar aceleración y cambios en la velocidad de rotación basados en el movimiento del mouse, en algunas pruebas las partículas se desorganizaban y perdían la estructura circular que deseaba.
- Otro reto fue la implementación de lerp() y lerpColor() de manera efectiva. Inicialmente, los cambios de radio y color eran demasiado abruptos, lo que hacía que la transición no se sintiera fluida.
¿Qué aprendiste de estos desafíos?
- La importancia de los pequeños ajustes: Experimenté con diferentes valores de aceleración y de interpolación hasta encontrar un equilibrio que mantuviera el patrón del iris sin romper la estética.
- Cómo hacer que la interacción se sienta natural: Aprendí que cambios demasiado bruscos en la velocidad pueden hacer que la animación se vea errática y mareadora, mientras que transiciones suaves con lerp() ayudan a mantener la fluidez.
- Optimización del código: Descubrí que ajustar el número de partículas visibles y limitar la frecuencia de ciertos cálculos ayuda a mantener un rendimiento estable sin comprometer el efecto visual.
Actividad 13
Conexión con Diseño de Entretenimiento Digital
Enunciado: describe cómo los conceptos de esta unidad pueden ser utilizados en el diseño de videojuegos, experiencias interactivas o animaciones. Da ejemplos concretos.
Entrega: descripción de al menos tres aplicaciones de los conceptos aprendidos en el diseño de entretenimiento digital, con ejemplos concretos.
🚀 Tu solución:
Conexión con Diseño de Entretenimiento Digital 🌜
Los conceptos de MOTION 101, aceleración, y lerp() pueden aplicarse de varias formas en el diseño de videojuegos, experiencias interactivas y animaciones. Aquí hay tres aplicaciones concretas:
1. Movimientos realistas en personajes y objetos
En un videojuego de plataformas, un personaje que salta puede usar aceleración constante para hacer que el salto se sienta más natural, en lugar de moverse a velocidad fija.
Ejemplo: En Super Mario Bros., Mario no alcanza su velocidad máxima de inmediato al correr, sino que acelera gradualmente.
2. Efectos visuales dinámicos y fluidos:
En animaciones de partículas, lerp() y lerpColor() ayudan a suavizar transiciones, como cambios de color en efectos de explosión o en iluminación ambiental.
Ejemplo: En un juego de magia, cuando un hechizo se carga, su color puede interpolar suavemente de azul a rojo, indicando su aumento de poder.
3. Interacciones intuitivas con el usuario:
En interfaces de usuario y experiencias interactivas, la interpolación con lerp() permite que los menús o elementos en pantalla se desplacen de manera fluida en vez de moverse bruscamente.
Ejemplo: En Fortnite, cuando un jugador abre el mapa, la cámara se desplaza suavemente hasta la posición deseada en lugar de moverse instantáneamente.
Actividad 14
Reflexión sobre el proceso de aprendizaje
Enunciado: reflexiona sobre tu propio proceso de aprendizaje durante esta unidad. ¿Qué estrategias te resultaron más efectivas para comprender los conceptos? ¿Qué podrías mejorar en futuras unidades?
Entrega:
- Descripción de las estrategias de aprendizaje utilizadas y su efectividad.
- Planteamiento de mejoras para futuras unidades.
🚀 Tu solución:
Reflexión sobre el proceso de aprendizaje
Primero que todo me gusto mucho esta unidad, fueron conceptos muy bacanos de aprender
- Aprender haciendo: Experimentar con el código y ver los efectos en tiempo real me ayudó mucho más que solo leer teoría. Ajustar valores, probar diferentes aceleraciones y usar lerp() y lerpColor() me hizo entender cómo funcionan en la práctica.
- Referentes visuales: Observar ejemplos de animaciones y simulaciones me dio ideas más claras de cómo aplicar los conceptos a mi propia aplicación.
- Iteración constante: Hacer pequeños cambios y probarlos en lugar de tratar de implementar todo de golpe me permitió identificar qué funcionaba y qué necesitaba ajustes.
Para mejorar en futuras unidades, quiero:
- Organizar mejor mis ideas antes de empezar a programar, para evitar rehacer muchas partes del código.
- Hacer una idea que se que pueda hacer viendo ejemplos claros
- De resto todo super.
Actividad 15
Autoevaluación
Enunciado: evalúa tu nivel de comprensión de los conceptos de la unidad en una escala del 1 al 5 (1: Nada de comprensión, 5: Dominio completo). Justifica tu autoevaluación con ejemplos concretos de tu trabajo en la unidad. Identifica áreas donde necesitas reforzar tu aprendizaje.
Entrega:
- Autoevaluación con justificación y ejemplos concretos de tu trabajo que sustenten.
- Identificación de áreas de mejora.
🚀 Tu solución:
Autoevaluación
Nivel de comprensión: 4/5
- Logré aplicar lerp(), lerpColor() y aceleraciones en mi simulación sin perder la esencia del diseño original.
- Implementé el marco MOTION 101 modelando partículas con posición, velocidad y aceleración, lo que hizo que el movimiento fuera más fluido y realista.
- Ajusté la rotación del iris en respuesta al movimiento del mouse, lo que demuestra comprensión de interacción y control dinámico.
Áreas de mejora:
- Optimizar el código para mejorar el rendimiento, ya que manejar muchas partículas puede afectar la fluidez.
- Explorar más formas de interpolación para darle más riqueza al movimiento de las partículas.