Unidad 1

Introducción

La aleatoriedad es un concepto fundamental en la simulación de sistemas interactivos, ya que permite modelar comportamientos impredecibles y variabilidad en los sistemas. En esta unidad, explorarás cómo generar y utilizar números aleatorios en tus simulaciones, comprendiendo su importancia y aplicaciones. A través de ejemplos como los paseos aleatorios, aprenderás a implementar movimientos y comportamientos que emulan la aleatoriedad presente en la naturaleza. Este conocimiento te proporcionará las herramientas necesarias para desarrollar simulaciones más realistas y dinámicas.

¿Qué aprenderás en esta unidad?

Vas a explorar la aleatoriedad como una herramienta fundamental en la simulación de sistemas interactivos. Esta herramienta te permitirá producir comportamientos impredecibles y variabilidad.

Actividad 01

Arte generativo

Enunciado: vas a observar con detenimiento los siguientes videos y vas a reflexionar la relación que esto podría tener con tu perfil profesional:

Entrega: escribe un texto corto donde expliques qué potencial crees que pueda tener el arte generativo y algorítmico en tu perfil profesional.

🚀 Tu solución:

El arte generativo y algorítmico combina creatividad y tecnología, lo que encaja perfecto con mi carrera en diseño de entretenimiento digital. La capacidad de crear patrones, animaciones y paisajes digitales únicos mediante el uso de código y algoritmos tiene un impacto significativo en áreas como la animación 3D, el diseño interactivo y la simulación de sistemas, especialmente en proyectos que busquen innovar en narrativas visuales. Ver cómo artistas como Refik Anadol usan datos y algoritmos para contar historias me inspira a aplicar estas ideas en proyectos creativos que conecten con el público de formas nuevas y emocionantes.

Actividad 02

Diseño generativo

Enunciado: vas a observar con detenimiento el siguiente video que habla acerca del diseño generativo

GENERATIVE DESIGN, INTRO & Patrik Hübner

Recursos:

Entrega: escribe un texto corto donde reflexiones acerca de esta pregunta ¿Cómo se conecta lo anterior como mis intereses? O tal vez ¿Esto abre la puerta a la exploración de otras posibilidades?

🚀 Tu solución:

El diseño generativo, como lo presenta Patrik Hübner, combina arte, datos y tecnología de formas únicas, lo que conecta con mi interés por la animación 3D y el modelado. Este enfoque abre nuevas posibilidades para contar historias visuales significativas, creando diseños que reaccionan a datos o entradas específicas. Además, su aplicación en branding me inspira para futuros proyectos, incluyendo el desarrollo visual de un emprendimiento, donde podría usar estos métodos para crear identidades dinámicas y personalizadas que reflejen la esencia de una marca. Esto no solo amplía mi creatividad, sino que también me permite explorar maneras innovadoras de impactar y enganchar al público de una forma diferente.

Investigación

Vas a indagar y a experimentar con los conceptos fundamentales de la unidad 0 del texto guía.

Actividad 03

Caminatas aleatorias

Enunciado: analiza el código del ejemplo Example 0.1: A Traditional Random Walk

Vas a realizar un experimento con el código:

Comprende el código, entiende lo que pasa y cómo se está aplicando el concepto.
Luego harás una modificación al código. Te harás esta pregunta ¿Qué pasaría si?
Trata de lanzar una hipótesis de lo que crees que ocurrirá.
Realiza la modificación.

Vas a documentar

Describe el experimento que vas a realizar.
¿Qué pregunta quieres responder con este experimento?
¿Qué resultados esperas obtener?
¿Qué resultados obtuviste?
¿Qué aprendiste de este experimento?

Entrega: los asuntos que te pido documentar en el enunciado, el código con las modificaciones y una captura de pantalla que muestre el resultado del experimento.

🚀 Tu solución:

Caminata aleatoria

Proceso en el que un “caminante” se mueve paso a paso en direcciones aleatorias dentro de un espacio definido. En cada paso, la dirección se elige al azar, y puede ser hacia arriba, abajo, izquierda o derecha (en el caso más simple). En programación, una caminata aleatoria se crea usando un bucle donde en cada iteración se calcula la nueva posición basándose en una dirección aleatoria. Esto genera trayectorias que pueden parecer caóticas o dispersas dependiendo de las reglas del movimiento.

Comprensión de código:

Clase Walker: Es el objeto principal que representa al “caminante”. Tiene dos propiedades (this.x y this.y) que marcan su posición actual en el lienzo, empezando en el centro.

Método step(): Define cómo se mueve el caminante.

Usa un número aleatorio entre 0 y 3 para decidir la dirección:

0: Mueve hacia la derecha (this.x++).

1: Mueve hacia la izquierda (this.x—).

2: Mueve hacia abajo (this.y++).

3: Mueve hacia arriba (this.y—).

Método show(): Dibuja un punto en la posición actual del caminante. Bucle draw():

Se ejecuta continuamente, haciendo que el caminante dé un paso (step()) y se dibuje en su nueva posición (show()).

// Declara una variable para almacenar el objeto "Walker"
let walker;

function setup() {
  // Crea un lienzo de 640x240 píxeles
  createCanvas(640, 240);

  // Inicializa un nuevo caminante (instancia de la clase Walker)
  walker = new Walker();

  // Establece el fondo en color blanco
  background(255);
}

function draw() {
  // Llama al método "step()" para que el caminante dé un paso
  walker.step();

  // Llama al método "show()" para dibujar al caminante en su nueva posición
  walker.show();
}

// Definición de la clase "Walker"
class Walker {
  // Constructor: inicializa la posición del caminante en el centro del lienzo
  constructor() {
    this.x = width / 2; // Coordenada X: mitad del ancho del lienzo
    this.y = height / 2; // Coordenada Y: mitad de la altura del lienzo
  }

  // Método "show()": dibuja al caminante en su posición actual
  show() {
    stroke(0); // Establece el color del punto en negro
    point(this.x, this.y); // Dibuja un punto en la posición actual (x, y)
  }

  // Método "step()": define cómo se mueve el caminante
  step() {
    // Genera un número entero aleatorio entre 0 y 3
    const choice = floor(random(4));

    // Elige una dirección de movimiento basada en el valor de "choice"
    if (choice == 0) {
      this.x++; // Si "choice" es 0, el caminante se mueve hacia la derecha (aumenta X)
    } else if (choice == 1) {
      this.x--; // Si "choice" es 1, el caminante se mueve hacia la izquierda (disminuye X)
    } else if (choice == 2) {
      this.y++; // Si "choice" es 2, el caminante se mueve hacia abajo (aumenta Y)
    } else {
      this.y--; // Si "choice" es 3, el caminante se mueve hacia arriba (disminuye Y)
    }
  }
}

Experimento

Voy a modificar el código para que el tamaño del punto cambie aleatoriamente en cada paso, asignando diferentes colores según el tamaño. Esto permitirá que el caminante deje trazos de tamaños y colores variados, lo que podría generar un patrón visual más dinámico y fácil de identificar.

¿Qué pregunta quieres responder con este experimento?

¿Cómo afecta la variación del tamaño de los puntos y su color a la visibilidad de los diferentes tamaños a lo largo de la caminata aleatoria?
¿Es fácil distinguir entre los diferentes tamaños de puntos en el canvas?

¿Qué resultados esperas obtener?

Espero ver una caminata aleatoria con puntos de tres tamaños (1, 2 y 3 píxeles) que sean claramente visibles y diferenciables por su color (rojo, verde y azul). Cada tamaño debería tener su propio color distintivo, lo que permitirá ver la evolución de la caminata de manera más clara.

Codigo:

El cambio se realizó en el método show(), añadiendo un tamaño aleatorio para el punto que dibuja el caminante entre 1 y 5.

let walker;

function setup() {
  createCanvas(640, 240);
  walker = new Walker();
  background(255);
}

function draw() {
  for (let i = 0; i < 10; i++) { // Hacer que dé 10 pasos por fotograma
    walker.step();
    walker.show();
  }
}

class Walker {
  constructor() {
    this.x = width / 2; // Inicia en el centro del lienzo
    this.y = height / 2;
  }

  show() {
    const size = random(1, 3); // Tamaño aleatorio entre 1 y 3
    let col;

    // Asignar un color según el tamaño
    if (size <= 1.5) {
      col = color(255, 0, 0); // Rojo para los puntos más pequeños (1 px)
    } else if (size <= 2.5) {
      col = color(0, 255, 0); // Verde para los puntos medianos (2 px)
    } else {
      col = color(0, 0, 255); // Azul para los puntos más grandes (3 px)
    }

    stroke(col); // Color del punto
    strokeWeight(size); // Ajusta el grosor del punto
    point(this.x, this.y); // Dibuja el punto en la posición actual
  }

  step() {
    const choice = floor(random(4)); // Elige una dirección aleatoria
    if (choice == 0) {
      this.x++;
    } else if (choice == 1) {
      this.x--;
    } else if (choice == 2) {
      this.y++;
    } else {
      this.y--;
    }
    // Limita al caminante dentro del canvas
    this.x = constrain(this.x, 0, width);
    this.y = constrain(this.y, 0, height);
  }
}

¿Qué resultados obtuviste?

Los puntos de tamaño 1, 2 y 3 píxeles son fácilmente distinguibles por su color (rojo, verde y azul, respectivamente). La caminata aleatoria ahora se representa con diferentes colores que corresponden a los tamaños de los puntos, lo que permite observar claramente cómo el caminante se desplaza a través del lienzo.

¿Qué aprendiste de este experimento?

Aprendí que al combinar variación en el tamaño y el color de los puntos, se mejora significativamente la visibilidad de los diferentes pasos en la caminata aleatoria. Esta modificación hace que sea mucho más fácil rastrear el movimiento del caminante, al mismo tiempo que agrega un componente visual interesante que hace que el experimento sea más dinámico y creativo. Además, experimenté cómo el tamaño y el color pueden influir en la percepción visual de una simulación interactiva.

Resultado:

Actividad 04

Distribuciones de probabilidad

Enunciado: analiza detenidamente este ejemplo.

En tus palabras cuál es la diferencia entre una distribución uniforme y una no uniforme de números aleatorios. Modifica el código de la caminata aleatoria para que utilice una distribución no uniforme, favoreciendo el movimiento hacia la derecha.

Entrega:

Explicación de la diferencia entre distribuciones uniformes y no uniformes.
Código modificado y captura de pantalla de la caminata con distribución no uniforme.

🚀 Tu solución:

Explicación de la diferencia entre distribuciones uniformes y no uniformes:

Distribución uniforme: Todos los números dentro de un rango tienen la misma probabilidad de ser seleccionados. En el código del ejemplo, random(100) genera números entre 0 y 100 con igual probabilidad, lo que distribuye los puntos de manera uniforme a lo largo de la línea horizontal.

Distribución no uniforme (gaussiana): Los números se distribuyen alrededor de un valor central (media) con una mayor probabilidad cerca de la media y menos probabilidad en los extremos. En el ejemplo, randomGaussian(50) genera números con una distribución alrededor del 50, lo que concentra más puntos cerca de ese valor, creando un agrupamiento central.

Codigo caminata con distribución no uniforme:

Este código genera una caminata no uniforme porque utiliza randomGaussian() para los movimientos horizontales (x), lo que genera un movimiento hacia la derecha, ya que los valores cercanos a la media (1) son más probables. En cambio, los movimientos verticales (y) usan random(), con una distribución uniforme y sin preferencia por ninguna dirección. Esto hace que el caminante se desplace más frecuentemente hacia la derecha, creando un patrón desequilibrado.

let walker;

function setup() {
  createCanvas(640, 240);
  walker = new Walker();
  background(255);
}

function draw() {
  walker.step();
  walker.show();
}

class Walker {
  constructor() {
    this.x = width / 2;
    this.y = height / 2;
  }

  show() {
    stroke(0);
    point(this.x, this.y);
  }

  step() {
    const stepX = randomGaussian(1, 1); // Favorece movimientos a la derecha (media 1)
    const stepY = random(-1, 1); // Distribución uniforme para movimientos verticales

    this.x += stepX;
    this.y += stepY;

    // Asegurar que se mantenga dentro de los límites
    this.x = constrain(this.x, 0, width);
    this.y = constrain(this.y, 0, height);
  }
}

Actividad 05

Distribución Normal

Enunciado: implementa un ejemplo que genere números aleatorios con una distribución normal (gaussiana). Visualiza la distribución utilizando figuras geométricas.

Entrega:

Código del ejemplo
Captura de pantalla
Una breve explicación de cómo se refleja la distribución normal en la visualización.

🚀 Tu solución:

Código del ejemplo

let values = [];

function setup() {
  createCanvas(640, 240);
  background(255);
  noStroke();
}

function draw() {
  // Generar un número aleatorio con distribución normal
  let num = randomGaussian(); // Media 0, desviación estándar 1

  // Escalar el número a un rango útil
  let sd = 60; // Desviación estándar
  let mean = width / 2; // Media
  let x = num * sd + mean;

  // Almacenar el valor
  values.push(x);

  // Limpiar la pantalla y graficar
  background(255);
  for (let i = 0; i < values.length; i++) {
    // Asignar un color aleatorio a cada círculo
    let r = random(255);
    let g = random(255);
    let b = random(255);
    fill(r, g, b, 150); // Color aleatorio con algo de transparencia

    // Dibujar el círculo
    ellipse(values[i], height / 2, 10, 10);
  }

  // Limitar la cantidad de valores para que no se acumulen infinitamente
  if (values.length > 1000) {
    values.shift();
  }
}

Captura de pantalla

Una breve explicación de cómo se refleja la distribución normal en la visualización

El código usa randomGaussian() para generar números con una distribución normal, centrados en 0. Estos números se escalan para que su media esté en el centro de la pantalla. Las posiciones de las figuras siguen esta distribución, por lo que se agrupan más cerca del centro y se dispersan menos hacia los bordes, creando una visualización de la forma de campana típica de la distribución normal.

Actividad 06

Distribución personalizada: Lévy flight

Enunciado: realiza una simulación donde visualices un salta de Lévy.

Entrega:

En qué consiste el concepto de Lévy flight y en qué caso sería interesante usarlo.
Código de la simulación.
Captura de pantalla.

🚀 Tu solución:

En qué consiste el concepto de Lévy flight y en qué caso sería interesante usarlo.

Un Lévy flight es un patrón de movimiento o de salto caracterizado por una secuencia de desplazamientos en los cuales los tamaños de los saltos siguen una distribución Lévy (una distribución de probabilidad con colas pesadas). Esta distribución se diferencia de la distribución normal porque tiene una mayor probabilidad de generar saltos muy largos en comparación con los saltos pequeños. Los saltos cortos son más frecuentes, pero las trayectorias pueden incluir desplazamientos muy grandes, lo que crea un patrón errático y no lineal.

¿Cuándo es interesante usarlo?

El Lévy flight es especialmente útil en modelos de búsqueda y exploración donde se quiere simular un comportamiento errático pero eficiente, como:

En biología, para modelar el movimiento de animales que buscan alimentos, como las abejas o algunos tipos de peces.
En algoritmos de optimización, como el Lévy flight search.
En física y estudios de difusión, como el movimiento de partículas en medios heterogéneos.

Código de la simulación.

let x, y;

function setup() {
  createCanvas(640, 240);
  x = width / 2;
  y = height / 2;
  background(255);
  noFill();
  stroke(0, 50, 255); // Línea de color
  frameRate(15); // Hacer que la animación sea moderadamente lenta
}

function draw() {
  // Simulación de Lévy flight
  let angle = random(TWO_PI); // Ángulo aleatorio
  let stepSize = pow(random(1), -1 / 1.5) * 30; // Aumentar el tamaño de los pasos

  // Calculando el nuevo desplazamiento
  let dx = cos(angle) * stepSize;
  let dy = sin(angle) * stepSize;

  // Dibujar línea desde la última posición hasta la nueva posición
  line(x, y, x + dx, y + dy);

  // Actualizando las posiciones
  x += dx;
  y += dy;

  // Dibujar un corazón en la nueva posición
  drawHeart(x, y);

  // Limitar la visualización a un tamaño de canvas
  if (x < 0 || x > width || y < 0 || y > height) {
    background(255); // Si se sale del canvas, reinicia
    x = width / 2;
    y = height / 2;
  }
}

// Función para dibujar un corazón
function drawHeart(x, y) {
  beginShape();
  vertex(x, y);
  bezierVertex(x - 10, y - 20, x - 30, y - 20, x - 30, y);
  bezierVertex(x - 30, y + 30, x, y + 50, x, y + 30);
  bezierVertex(x + 30, y + 50, x + 30, y + 30, x + 30, y);
  bezierVertex(x + 30, y - 20, x + 10, y - 20, x, y);
  endShape(CLOSE);
}

Captura de pantalla.

Actividad 07

Ruido Perlin

Enunciado: utiliza el ruido Perlin para generar variaciones aleatorias pero suaves. Construye una aplicación que permita visualizar lo anterior.

Entrega:

Explica en tus propias palabras la figura 0.4: “A graph of Perlin noise values over time (left) and of random noise values over time (right)”
Explica cómo usaste el ruido Perlin para generar las variaciones.
El código.
Una captura de pantalla que muestre la visualización generada.

🚀 Tu solución:

Explicación

A graph of Perlin noise values over time (left) and of random noise values over time (right)”

Figura 0.4:

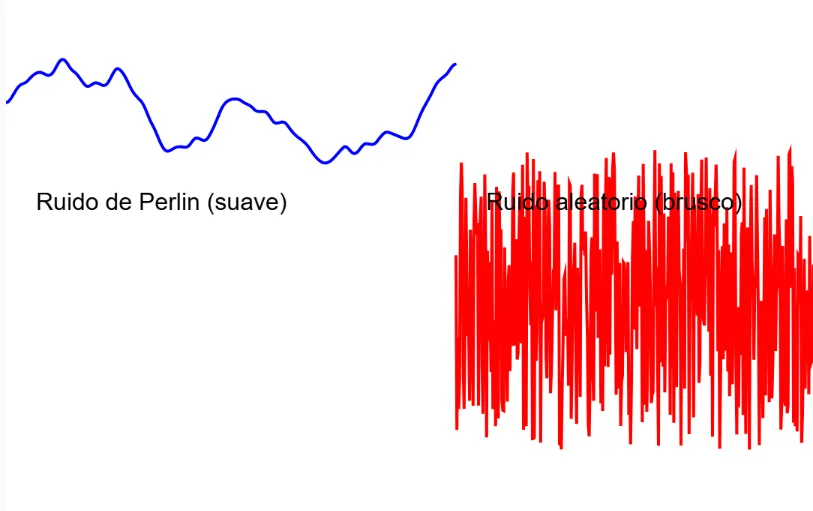
Gráfico izquierdo (ruido de Perlin): Este gráfico muestra cómo los números cambian de manera suave y continua. Los valores no son totalmente aleatorios, sino que están relacionados entre sí. Es como si los números “trabajaran en equipo” para formar una línea fluida, como las olas del mar o el relieve de una montaña.Este comportamiento es ideal para simular fenómenos naturales.

Gráfico derecho (aleatoriedad uniforme): Representa una secuencia de valores puramente aleatorios, donde cada número no tiene relación con los demás. Esto muestra un gráfico irregular, con saltos bruscos entre los puntos. Aquí los números cambian de forma caótica y desordenada.

En resumen, el gráfico de la izquierda muestra variaciones más naturales y orgánicas, mientras que el de la derecha es más caótico.

Explica cómo usaste el ruido Perlin para generar las variaciones.

En el código, use dos tipos de ruido para generar variaciones en la altura de los puntos en las dos gráficas que se dibujan en el lienzo: ruido Perlin (suave) y ruido aleatorio (brusco).

1. Ruido Perlin:

En la función dibujarRuidoPerlin(), utilice el ruido Perlin para generar una línea suave y fluida. El ruido Perlin se utiliza para determinar las variaciones en el eje Y de cada punto, generando un cambio gradual entre los puntos.

let y = noise(i * scale) * 150 + yOffset;

noise(i * scale): Aquí utilice la función noise() de p5.js, que genera valores continuos (sin saltos abruptos). Al multiplicar i (el índice del punto) por scale (0.01), controlamos la “resolución” de la variación del ruido. Un valor pequeño de scale como este hace que las variaciones sean suaves y amplias.
*150: Escala el valor generado por noise() para aumentar la amplitud de las variaciones en el eje Y. El rango de variación se extiende entre 0 y 150 píxeles verticalmente.
+ yOffset: Desplaza la línea en el eje Y, asegurando que la línea no quede demasiado cerca de los bordes del canvas. Esta variación suave se genera porque el ruido Perlin produce cambios continuos y graduales, lo que da lugar a una línea que parece más natural y orgánica.

2. Ruido Aleatorio:

En la función dibujarRuidoAleatorio(), se genera una variación más brusca usando valores aleatorios. Aquí, los puntos en la línea se colocan en posiciones Y aleatorias dentro de un rango determinado.

let y = random(height / 4, (3 * height) / 4);

random(height / 4, (3 * height) / 4): En lugar de usar noise(), aquí se usa la función random() para generar valores completamente aleatorios. Estos valores se ubican entre height / 4 y (3 * height) / 4, lo que significa que los puntos se distribuyen de manera aleatoria dentro de la mitad del canvas verticalmente.
Como el ruido aleatorio no tiene en cuenta las posiciones anteriores, genera un comportamiento más “caótico” y con saltos bruscos entre los valores de y.

Código

let numPoints = 500; // Número de puntos en la línea
let scale = 0.01; // Escala del ruido Perlin
let yOffset = 150; // Posición base en Y

function setup() {
  createCanvas(600, 400); // Tamaño del canvas
  background(255); // Fondo blanco
  strokeWeight(2); // Grosor de las líneas
  noLoop(); // Solo se ejecuta una vez
}

function draw() {
  background(255); // Limpiar la pantalla

  // Dibujar las líneas de ruido en dos secciones
  dibujarRuidoPerlin(0, 0); // Dibuja la gráfica de ruido Perlin en la mitad izquierda
  dibujarRuidoAleatorio(width / 2, 0); // Dibuja la gráfica de ruido aleatorio en la mitad derecha

  // Etiquetas
  dibujarEtiquetas();
}

function dibujarRuidoPerlin(xOffset, yOffset) {
  stroke(0, 0, 255); // Azul
  noFill();
  beginShape();
  for (let i = 0; i < numPoints; i++) {
    let x = map(i, 0, numPoints, 0, width / 2); // Usamos solo la mitad del ancho
    let y = noise(i * scale) * 150 + yOffset;
    vertex(x + xOffset, y);
  }
  endShape();
}

function dibujarRuidoAleatorio(xOffset, yOffset) {
  stroke(255, 0, 0); // Rojo
  beginShape();
  for (let i = 0; i < numPoints; i++) {
    let x = map(i, 0, numPoints, 0, width / 2); // Usamos solo la mitad del ancho
    let y = random(height / 4, (3 * height) / 4); // Valores aleatorios
    vertex(x + xOffset, y);
  }
  endShape();
}

function dibujarEtiquetas() {
  fill(0);
  noStroke();
  textSize(16);
  text("Ruido de Perlin (suave)", 20, yOffset - 10);
  text("Ruido aleatorio (brusco)", width / 2 + 20, yOffset - 10);
}

Captura

Aplicación

Vas a aplicar los conceptos con los que experimentaste en la fase de investigación para diseñar y desarrollar una aplicación interactiva en tiempo real.

Actividad 08

Diseño: exploración de la idea

Enunciado: diseña una aplicación interactiva en tiempo que utilice los conceptos que investigaste. La aplicación debe:

Generar una pieza de arte generativo algorítmico.
Debes usar al menos TRES conceptos.
El contenido generado debe ser interactivo. Puedes utilizar mouse, teclado, cámara, micrófono, etc, para variar los parámetros del algoritmo en tiempo real.

Entrega:

Un texto donde expliques tu intención de diseño.
¿Cómo piensas usar los tres conceptos y por qué estos?
Reporta los referentes que usaste para inspirarte.

🚀 Tu solución:

Un texto donde expliques tu intención de diseño.

El objetivo de esta aplicación es crear una pieza de arte generativo algorítmico que represente el movimiento suave y orgánico de las olas del mar. La visualización busca capturar la estética del agua a través de movimientos ondulantes y colores que reflejen diferentes tonalidades de azul. La interacción en tiempo real permite que el usuario controle la velocidad, la intensidad del movimiento de las olas y su altura, generando una experiencia única cada vez que se usa.

Interaccion: Teclas izquierda/derecha: Controlan la velocidad del movimiento de las partículas (olas). Mouse: Modifica la altura máxima de las olas. Mover el mouse hacia arriba o hacia abajo permite ajustar la “fuerza” de las olas, haciéndolas más altas o más bajas.

¿Cómo piensas usar los tres conceptos y por qué estos?

Arte Generativo Algorítmico: La composición visual está creada mediante múltiples “partículas” (bolas) que simulan olas dinámicas. El arte es generado por el algoritmo en tiempo real, y su comportamiento cambia según la interacción del usuario. El movimiento fluido y estético de las partículas asegura que el diseño sea visualmente agradable y evocador.

Distribución Normal: Las posiciones y tamaños de las bolas están generados con ligeras variaciones, simulando una distribución donde la mayoría de las bolas tienen un tamaño promedio, pero algunas se destacan con tamaños mayores o menores. Esto crea una composición natural y orgánica.

Ruido Perlin: Las trayectorias de las partículas están controladas por ruido Perlin, lo que genera movimientos suaves y continuos en lugar de un desplazamiento caótico. Este ruido permite que las bolas se desplacen como si estuvieran empujadas por el flujo del agua, recreando las olas de forma realista.

Reporta los referentes que usaste para inspirarte.

Generative Art by Casey Reas: Su trabajo con algoritmos simples para crear composiciones visuales complejas me inspiró a combinar matemáticas y arte.

Tyler Hobbs: es conocido por sus composiciones generativas que utilizan algoritmos para crear patrones visuales complejos, con un enfoque en la aleatoriedad y la organización visual.

“The Coding Train” por Daniel Shiffman: Sus exploraciones sobre ruido Perlin y partículas inspiraron la idea de utilizar este ruido para simular olas de forma fluida y orgánica.

Referencias visuales de acuarelas de olas: Obras visuales que simulan el mar a través de suaves cambios de tonalidad y textura.

Actividad 09

Materialización

Enunciado: vas a implementar tu aplicación diseñada.

Entrega:

Código de la aplicación.
Captura del contenido generado.
En caso de realizar alguna variación al concepto original, escribe un texto donde expliques la razón del cambio.

🚀 Tu solución:

Código de la aplicación.

let waveSpeed = 0.03;  // Velocidad de las olas
let waveHeight = 300;  // Altura de las olas
let waveIntensity = 1; // Intensidad de las olas
let noiseOffset = 0;   // Desplazamiento de ruido Perlin
let numWaves = 20     // Número de filas de olas
let numParticles = 100; // Más partículas para llenar la ola
let numSandParticles = 200; // Partículas de arena

let shapeType = 'circle'; // Forma predeterminada de las partículas

function setup() {
  createCanvas(windowWidth, windowHeight);
  noStroke();
}

function draw() {
  // Fondo completamente azul (más oscuro)
  background(0, 102, 204);  // Azul más oscuro para el mar

  // Dibujar las olas
  for (let i = 0; i < numWaves; i++) {
    drawWave(i * 100);  // Llamar a la función que dibuja cada ola
  }

  // Movimiento de las olas: modificar la posición de las olas con el tiempo
  noiseOffset += waveSpeed;

  // Dibujar las partículas de arena en la parte inferior
  drawSandParticles();
}

function drawWave(offset) {
  // Ajustamos la altura de las olas con el mouse
  let waveHeightMod = map(mouseY, 0, height, 50, waveHeight);
  let waveIntensityMod = map(mouseX, 0, width, 0.5, waveIntensity);

  // Dibujar las partículas que simulan las olas
  for (let i = 0; i < numParticles; i++) {
    let x = 150 * randomGaussian() + width / 2;  // Aumentar la dispersión de partículas
    x = constrain(x, 0, width);  // Limitar la posición a la pantalla

    // Usamos ruido Perlin para las posiciones verticales de las partículas
    let y = height / 2 + sin(TWO_PI * (x / width) + noise(x * 0.01 + noiseOffset) * waveIntensityMod) * waveHeightMod;

    // Tamaño de las partículas basado en el ruido
    let size = map(noise(x * 0.05 + noiseOffset), 0, 1, 10, 20);

    // Gradiente de azul para las partículas con tonalidades variadas
    let baseColor = map(sin(x * 0.1), -1, 1, 0, 255);  // Base para la variación
    let color1 = map(baseColor, 0, 220, 100, 90);  // Azul más claro
    let color2 = map(baseColor, 0, 180, 150, 216);   // Azul más oscuro

    fill(color1, color2, 220, 150);  // Gradiente de azul en la partícula

    // Cambiar la forma de la partícula según `shapeType`
    if (shapeType === 'circle') {
      ellipse(x, y + offset, size, size);  // Círculo
    } else if (shapeType === 'square') {
      rect(x - size / 2, y + offset - size / 2, size, size);  // Cuadrado
    } else if (shapeType === 'triangle') {
      triangle(
        x, y + offset - size / 2,  // Parte superior
        x - size / 2, y + offset + size / 2,  // Esquina izquierda
        x + size / 2, y + offset + size / 2   // Esquina derecha
      );  // Triángulo
    }
  }
}

function drawSandParticles() {
  // Partículas de arena en la parte inferior de la pantalla
  for (let i = 0; i < numSandParticles; i++) {
    let x = random(width);  // Posición aleatoria en el eje X
    let y = random(height / 2, height);  // Posición aleatoria en la parte inferior

    // Tamaño aleatorio para las partículas de arena
    let size = random(3, 6);

    // Color beige para simular arena
    fill(255, 229, 153, 180);  // Color beige con algo de transparencia

    // Dibujar la partícula de arena
    ellipse(x, y, size, size);
  }
}

function keyPressed() {
  // Modificar la velocidad de las olas con las teclas izquierda/derecha
  if (keyCode === LEFT_ARROW) {
    waveSpeed -= 0.05
  } else if (keyCode === RIGHT_ARROW) {
    waveSpeed += 0.03
  }

  // Cambiar la forma de las partículas al presionar la barra espaciadora
  if (keyCode === 32) { // Código de la barra espaciadora
    let randomShape = random();  // Generar un valor aleatorio entre 0 y 1
    if (randomShape < 0.33) {
      shapeType = 'circle';  // Seleccionar círculo
    } else if (randomShape < 0.66) {
      shapeType = 'square';  // Seleccionar cuadrado
    } else {
      shapeType = 'triangle';  // Seleccionar triángulo
    }
  }
}

Captura del contenido generado.

Cambios

Ninguno por el momento, quede contenta por asi decirlo, pues fue mas por lo grafico.

Consolidación y matacognión

Ahora que has experimentado con la aleatoriedad y has aplicado estos conceptos en una pieza de arte generativo, es momento de reflexionar sobre el proceso y los resultados obtenidos.

Actividad 10

Análisis de resultados

Enunciado: revisa los resultados de las actividades de la fase APPLY. ¿Qué desafíos encontraste al aplicar los conceptos aprendidos? ¿Qué aprendiste de estos desafíos?

Entrega: descripción de los desafíos encontrados y las lecciones aprendidas durante la fase APPLY.

🚀 Tu solución:

¿Qué desafíos encontraste al aplicar los conceptos aprendidos?

Tuve muchas dificultades con el codigo, no sabia que idea hacer, que fuera interesante y realmente cautivadora. Para lograr un movimiento de olas natural y fluido fue un reto porque al principio parecían moverse de manera rígida o demasiado uniforme. La solución fue usar ruido Perlin (noise()) en lugar de funciones trigonométricas simples, lo que permitió un desplazamiento más natural.

¿Qué aprendiste de estos desafíos?

1. La importancia de la distribución de datos

Experimentar con random() y randomGaussian() ayudó a comprender cómo la distribución de partículas afecta la percepción visual del movimiento y la profundidad en una simulación.

2. Cómo pequeños detalles mejoran la estética

Ajustar colores, tamaños de partículas y niveles de transparencia hizo que la animación se sintiera más dinámica y atractiva visualmente.

Interacción y control en tiempo real

Aprender a modificar valores con el teclado y el mouse permitió agregar una capa de interactividad que hace que la simulación sea más inmersiva y adaptable.

Actividad 11

Conexión con Diseño de Entretenimiento Digital

Enunciado: describe cómo los conceptos de aleatoriedad, distribuciones y ruido Perlin pueden ser utilizados en el diseño de videojuegos, experiencias interactivas o animaciones. Da ejemplos concretos.

Entrega: descripción de al menos tres aplicaciones de los conceptos aprendidos en el diseño de entretenimiento digital, con ejemplos concretos.

🚀 Tu solución:

Conexión con Diseño de Entretenimiento Digital 🍨

En el diseño de videojuegos, experiencias interactivas y animaciones, los conceptos de aleatoriedad, distribuciones y ruido Perlin juegan un papel clave en la creación de entornos más dinámicos, naturales e inmersivos.

Descripción de tres aplicaciones de los conceptos aprendidos en el diseño de entretenimiento digital, con ejemplos concretos.

1. Generación Procedural de Terrenos y Mapas 🗺️ En muchos videojuegos, los mundos abiertos y los niveles generados proceduralmente utilizan ruido Perlin para crear terrenos realistas. A diferencia de la aleatoriedad pura, que genera cambios bruscos, el ruido Perlin produce variaciones suaves y continuas, ideal para representar montañas, ríos y biomas.

Ejemplo: En Minecraft, el terreno se genera a partir de funciones de ruido Perlin y Simplex, lo que permite que las colinas, cuevas y océanos tengan una transición suave y orgánica.

2. Animaciones y Movimientos Naturales 🫀 Las animaciones en videojuegos y experiencias interactivas pueden beneficiarse de la aleatoriedad controlada para dar una sensación más realista. El ruido Perlin se usa para simular movimientos suaves y naturales, evitando el efecto mecánico de interpolaciones lineales.

Ejemplo: En juegos como The Legend of Zelda: Breath of the Wild, el balanceo de la hierba y las hojas responde a un patrón de viento generado con ruido Perlin, lo que hace que el ambiente se sienta más vivo.

3. Distribución de Objetos y NPCs en Escenarios 🏙️ En el diseño de niveles y experiencias interactivas, es importante que los objetos, enemigos o NPCs (personajes no jugables) no aparezcan de forma completamente aleatoria, sino con una distribución que se sienta natural. Las distribuciones normales (gaussianas) ayudan a colocar elementos con mayor concentración en ciertas áreas y menor densidad en otras.

Ejemplo: Se aplica en Brawl Stars en el matchmaking, donde los jugadores son emparejados con oponentes de niveles similares según distribuciones estadísticas.

Actividad 12

Reflexión sobre el proceso de aprendizaje

Enunciado: reflexiona sobre tu propio proceso de aprendizaje durante esta unidad. ¿Qué estrategias te resultaron más efectivas para comprender los conceptos? ¿Qué podrías mejorar en futuras unidades?

Entrega:

Descripción de las estrategias de aprendizaje utilizadas y su efectividad.
Planteamiento de mejoras para futuras unidades.

🚀 Tu solución:

Descripción de las estrategias de aprendizaje utilizadas y su efectividad.

Chatgpt y yo best friends forever, me gusta la forma en que me ayuda a comprender conceptos muy complejos para mi, de una forma mas natural o facil de entender. Explica de forma clara y me permite hacer preguntas sin presión, lo que facilita mi aprendizaje.
Comprendo mejor cuando veo los resultados en acción. A veces los conceptos teóricos no los entiendo del todo, pero al verlos aplicados en ejemplos visuales, todo tiene más sentido.

Planteamiento de mejoras para futuras unidades.

No ninguna, siento que el curso esta muy bien planeado

Actividad 13

Autoevaluación

Enunciado: evalúa tu nivel de comprensión de los conceptos de la unidad en una escala del 1 al 5 (1: Nada de comprensión, 5: Dominio completo). Justifica tu autoevaluación con ejemplos concretos de tu trabajo en la unidad. Identifica áreas donde necesitas reforzar tu aprendizaje.

Entrega:

Autoevaluación con justificación y ejemplos concretos.
Identificación de áreas de mejora.

🚀 Tu solución:

Autoevaluación con justificación y ejemplos concretos.

📊 Nivel de comprensión: 4/5

Siento que entendí bien los conceptos de aleatoriedad, distribuciones y ruido Perlin porque los apliqué en mi simulación de olas en p5.js y fueron los que me parecieron los mas intersantes. Logré que las olas se movieran de forma natural, usando distribución normal para las partículas y ruido Perlin para que el movimiento fuera más fluido.

Me encanto también la Caminata aleatoria en donde un “caminante” se mueve paso a paso en direcciones aleatorias dentro de un espacio definido. En cada paso, la dirección se elige al azar, y puede ser hacia arriba, abajo, izquierda o derecha, y puede crear cosas visualmente muy lindas.
Creo que el que menos entendí fue el de Lévy flight

Identificación de áreas de mejora.

Optimización del código: A veces no sé si mi código es eficiente o si hay formas mejores de hacerlo.
Más experimentación visual
En manejo del tiempo.
En general, me siento cómoda con los temas, pero necesito más práctica para aplicarlos de forma más creativa y eficiente.